Eyeballing Ihr Augapfel-Rezept: ein BME60B-Projekt - Gunook

2024 Autor: John Day | [email protected]. Zuletzt bearbeitet: 2024-01-30 07:15

Von: Hannah Silos, Sang Hee Kim, Thomas Vazquez, Patrick Viste

Die Vergrößerung ist eines der wichtigsten Merkmale von Lesebrillen, die nach ihrer Dioptrien-Verordnung klassifiziert werden. Laut der Michigan Technology University ist eine Dioptrie eine Brennweite des Objektivs, die normalerweise in mm gemessen wird, in der Einheit Meter (Michigan Technology University). Da Lesebrillen konvexe Linsen haben, wäre die Brennweite positiv, wodurch auch die Dioptrien positiv sind (HyperPhysik). Die Brennweite nimmt mit zunehmender Entfernung des Objekts von der eigentlichen Linse zu, was dazu führt, dass die Dioptrien kleiner werden, da sie umgekehrt proportional sind. Daher würde eine Lesebrille mit zusätzlichen Dioptrien dem Objektiv helfen, die Ansicht zu vergrößern, sodass es den Anschein hat, dass die Brennweite geringer ist, indem der Wert der Dioptrien erhöht wird.

Der vorgestellte Code wird verwendet, um die Dioptrie einer Linse mit einer unbekannten Sehstärke vorherzusagen. Zur Berechnung der Rezeptur werden zwei Eingaben verwendet: ein Foto des kontrollierten Hintergrunds ohne Verwendung von Objektiven und ein weiteres Foto des gleichen Hintergrunds, aber durch das Objektiv Ihrer Wahl. Das Programm misst die Verzerrung zwischen diesen beiden Fotos. Von dort aus können wir die Dioptrie der Linse abschätzen und ein Ergebnis für den Benutzer erstellen.

Für dieses Instructable benötigen Sie:

• Ein schwarz-weißes Schachbrettmuster, gedruckt auf ein 11 x 8,5 Zoll großes Blatt Papier
• Eine Kamera mit der Fähigkeit, ihren Fokus zu fixieren
• Ein Stativ oder ähnliches, um die Kamera zu sichern
• Verschiedene Rezepte von Lesebrillen
• MATLAB

Schritt 1: Machen Sie Fotos

Um die Vergrößerung einer Linse zu berechnen, müssen Sie sie mit der tatsächlichen Größe des Objekts vergleichen können. Für dieses Projekt vergleichen wir ein vergrößertes Bild mit einem Kontrollbild.

Der erste Schritt besteht also darin, zwei Fotos desselben Bildes zu machen – das erste nur durch die Kamera und das zweite durch das Objektiv der Lesebrille, die Sie testen möchten.

Sie machen ein Bild von einem 8,5 x 11 Zoll Schwarz-Weiß-Schachbrett mit einem 1 Zoll Raster. Stellen Sie Ihre Kamera 11 Zoll vom Schachbrett entfernt auf. Fixieren Sie den Fokus auf dem Schachbrett, bevor Sie die Fotos aufnehmen.

Machen Sie ein Foto vom Schachbrett ohne Lesebrille. Stellen Sie dann, ohne etwas zu bewegen, die Lesebrille vor die Kamera und machen Sie das zweite Foto.

Stellen Sie sicher, dass sich die Position Ihrer Kamera zwischen den Aufnahmen nicht bewegt. Das einzige, was sich zwischen den beiden Fotos ändern sollte, ist das Vorhandensein der Brillenlinse vor der Kamera.

Wenn Sie mit den Fotos fertig sind, laden Sie sie auf Ihren Computer hoch.

Schritt 2: Laden Sie die Bilder in MATLAB

Öffnen Sie ein neues Skript.

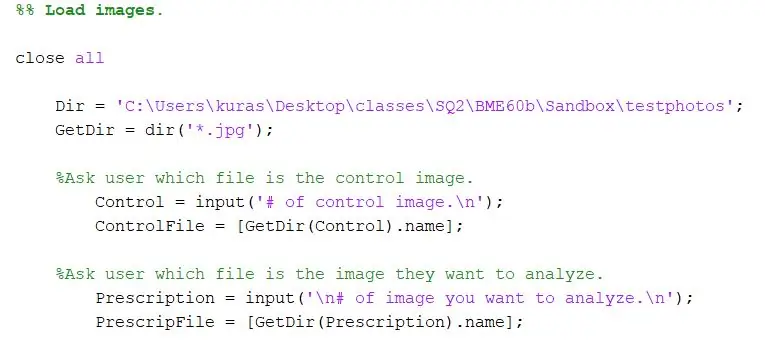
Geben Sie zunächst das Verzeichnis an, in dem die Fotos gespeichert werden. Verwenden Sie dann die dir-Funktion, um.jpg-Bilder (oder den Dateityp Ihres Bildes) zu extrahieren.

Dir = 'C:\Benutzer\kuras\Desktop\classes\SQ2\BME60b\Sandbox\testphotos'; GetDir = dir('*.jpg');

Für unser Projekt wollten wir den Benutzer des Programms auffordern, für welche Dateien er vergleichen möchte. Der erste Abschnitt fordert den Benutzer auf, das Kontrollbild anzugeben, und der zweite Abschnitt fordert den Benutzer auf, das Testbild anzugeben.

• %Fragen Sie den Benutzer, welche Datei das Kontrollbild ist.
• Control = input('# des Kontrollbildes.\n');
• ControlFile = [GetDir(Control).name]
• %Fragen Sie den Benutzer, welche Datei das Bild ist, das er analysieren möchte.
• ChooseFile = input('\n# des zu analysierenden Bildes.\n');
• PrescripFile = [GetDir(ChooseFile).name];

Schritt 3: Bildanalyse

Ein Farbbild in MATLAB hat die Größe MxNx3, während ein Graustufenbild MxN hat. Dies bedeutet, dass es schneller ist, ein Graustufenbild zu verbessern/zu bearbeiten, da weniger Daten zu verfolgen sind. Verwenden Sie rgb2gray, um das Bild in Graustufen zu konvertieren. (Die Imrotate-Funktion wurde verwendet, weil unsere Fotos horizontal waren - diese Codezeile kann in Ihrer Version erforderlich sein oder nicht.)

• %in Graustufen umwandeln und drehen
• I = imread(ControlFile);
• I = rgb2gray(I);
• I = imrotieren (I, 90);

Als nächstes zeigen Sie das Bild an. Die Subplot-Funktion wird verwendet, damit das Testbild in späteren Schritten neben der Steuerung angezeigt werden kann.

• %Anzeige
• Abbildung 1);
• Nebenhandlung(1, 2, 1)
• imshow(I);
• Titel (Kontrolldatei);

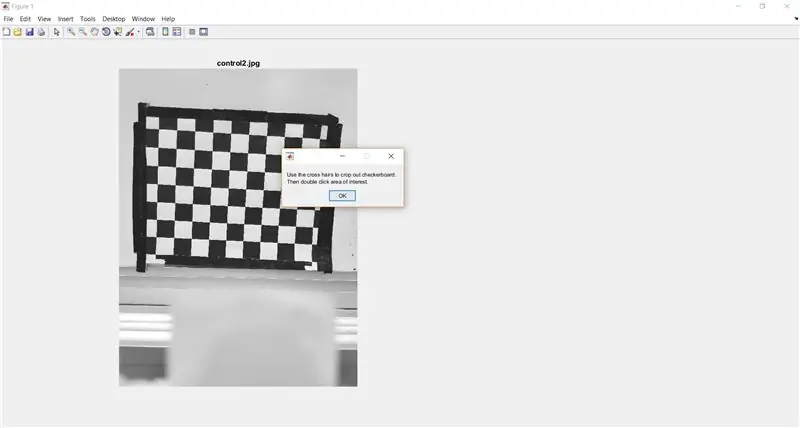
Verwenden Sie imcrop, um den Benutzer aufzufordern, das Schachbrett aus dem Vollbild zuzuschneiden. Der folgende Code zeigt auch ein Meldungsfeld an, um dem Benutzer Anweisungen zu geben.

• % Schachbrett zur Analyse ausschneiden
• waitfor(msgbox({'Verwenden Sie das Fadenkreuz, um das Schachbrett auszuschneiden.', 'Dann doppelklicken Sie auf den gewünschten Bereich.'}));
• I_crop = imcrop(I);

Verwenden Sie imbinarize, um das Bild zu binarisieren.

I_binary = imbinarize(I_crop);

Schritt 4: Berechnen Sie die Breite der weißen Quadrate auf dem Schachbrett

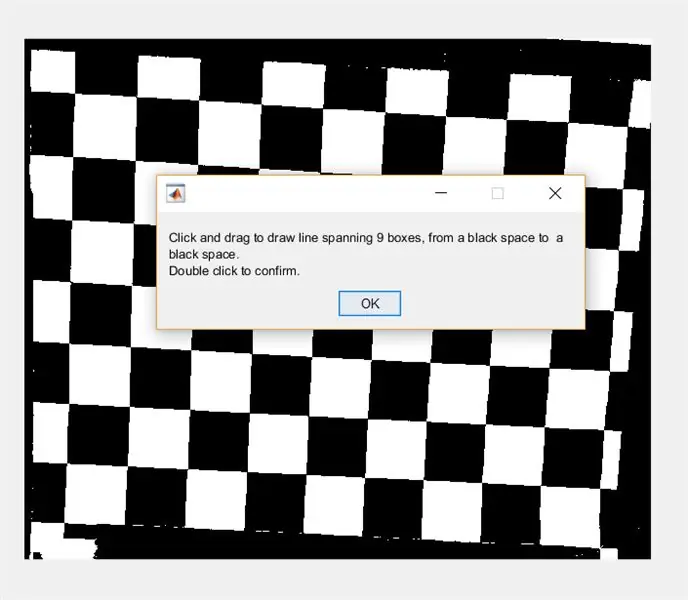
Fordern Sie den Benutzer als Nächstes auf, mit imline eine Linie durch das Bild zu ziehen. Diese Linie sollte horizontal über das Schachbrett verlaufen. Es sollte auf einem schwarzen Quadrat beginnen und enden (egal wo) - das liegt daran, dass wir die Breite der weißen Quadrate messen, nicht die der schwarzen.

• %Linie zeichnen
• Abbildung 1)
• Nebenhandlung(1, 2, 1)
• imshow(I_binary);
• waitfor(msgbox({'Klicken und ziehen, um eine Linie zu zeichnen, die 9 Felder umfasst, von einem schwarzen Raum zu einem schwarzen Raum.', 'Doppelklick zur Bestätigung.'}));
• Linie = imline;
• Position = warten(Zeile);
• Endpunkte = line.getPosition;

Extrahieren Sie die X- und Y-Koordinaten für die Endpunkte der gezeichneten Linie.

• X = Endpunkte(:, 1)
• Y = Endpunkte (:, 2);

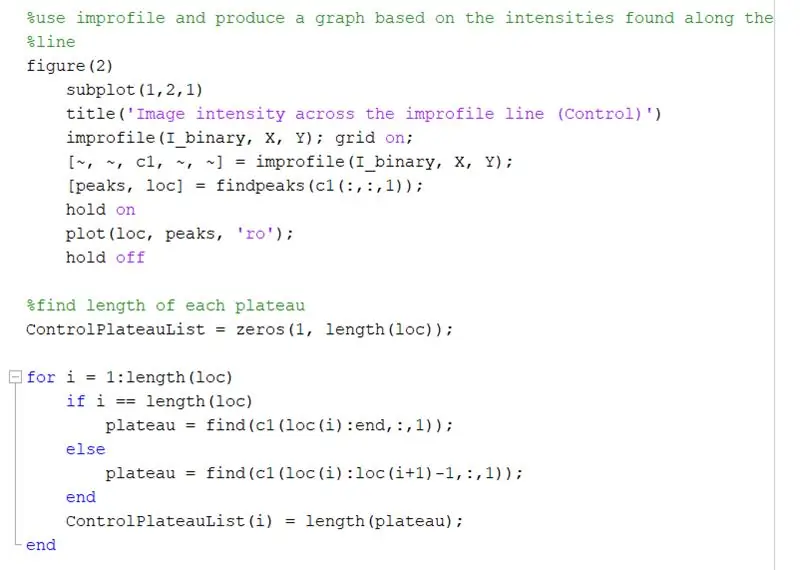
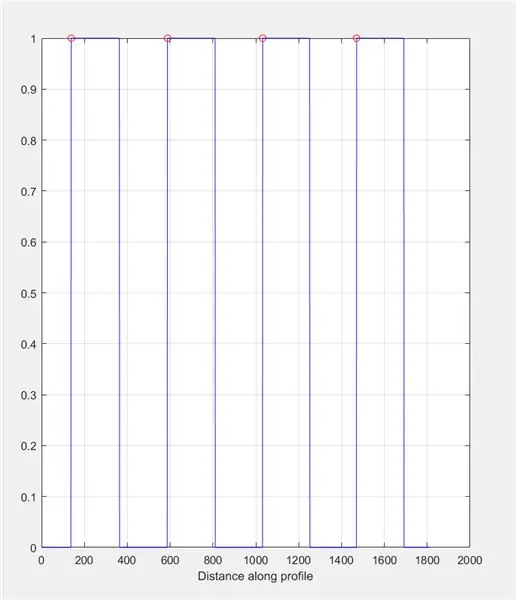
Verwenden Sie improfile, um ein Diagramm zu erstellen, das auf den Intensitäten basiert, die entlang der gezeichneten Linie gefunden wurden. Dies sollte einer Rechteckwelle im Bereich von 0 (schwarz) bis 1 (weiß) ähneln. Berechnen Sie auch die Peaks und ihre Lage.

• Figur 2)
• Nebenhandlung(1, 2, 1)
• title('Bildintensität über die Profillinie (Kontrolle)')
• improfile(I_binary, X, Y); Gitter an;
• [~, ~, c1, ~, ~] = improfile(I_binary, X, Y);
• [peaks, loc] = findpeaks(c1(:,:, 1));
• festhalten
• plot(loc, Peaks, 'ro');
• warte ab

Ermitteln Sie die Länge jedes Plateaus im Improfile-Diagramm mithilfe einer for-Schleife. Führen Sie die for-Schleife für die gleiche Anzahl von Peaks aus, die im Improfile-Diagramm vorhanden sind. Um die Länge jedes Plateaus zu berechnen, verwenden Sie die Funktion „Suchen“, um alle Stellen zu finden, an denen ein Intensitätswert von „1“anstelle von „0“vorhanden ist. Berechnen Sie dann die Länge dieses Arrays, um die Gesamtlänge des Plateaus zu erhalten, die der Breite eines weißen Quadrats in Pixeln entsprechen sollte. ControlPlateauList = zeros(1, length(loc));

für i = 1:Länge(loc)

wenn ich == Länge (loc)

Plateau = find(c1(loc(i):end,:, 1));

anders

Plateau = find(c1(loc(i):loc(i+1)-1,:, 1));

Ende

ControlPlateauList(i) = Länge(Plateau);

Ende

Schritt 5: Wiederholen Sie die Schritte 3 und 4 für das Testbild

*Hinweis: Achten Sie beim Zeichnen der unprofilierten Linie auf dem Testbild darauf, diese über die Quadrate zu ziehen, die der Linie entsprechen, die Sie auf dem Kontrollbild gezeichnet haben.

Schritt 6: Berechnen Sie die Vergrößerung des Objektivs

Die vergrößerten Messungen werden berechnet, indem der Mittelwert der Länge des Plateaus, der in Schritt 5 berechnet wurde, durch den Mittelwert der Länge des Kontrollplateaus, der in Schritt 4 berechnet wurde, dividiert wird. Dies wird zu 1,0884 berechnet.

Vergrößerung = mean(plateauList)/mean(ControlPlateauList);

Schritt 7: Finden von R-Quadrat und der Verschreibung des Benutzers durch Interpolation

Verwenden des Codes:

• md1 = fitlm(Vorgabe, MagArray);
• Rsquared = md1. Rsquared. Ordinary;

Wir können den R-Quadrat-Wert des Graphen GivenPresciption (von unseren Linsen gegebene Werte) vs. MagArray (ein Array der zuvor berechneten Vergrößerungsmessverhältnisse) ermitteln. Durch einen ausreichend hohen R-Quadrat-Wert kann gefolgert werden, dass eine ausreichend starke Korrelation besteht, um die Verwendung dieses Verfahrens zu rechtfertigen. Für diesen speziellen Fall betrug der R-Quadrat-Wert 0,9912, was auf eine starke Korrelation hindeutet und daher die Verwendung dieser Methode in der Analyse gerechtfertigt ist.

Verwenden der Funktion:

Prescription = interp1(MagArray, GivenPrescription, Vergrößerung, 'linear');

Wir können den entsprechenden Verschreibungswert (auf der x-Achse) unseres Vergrößerungsverhältnisses (einen Wert auf der y-Achse) interpolieren und die Verschreibung des Benutzers ermitteln.

Die Interpolation von Daten ist für das Funktionieren dieser Methode wichtig, da sie es uns ermöglicht, Annahmen über Informationen zu treffen, die wir nicht haben, basierend auf den Informationen, die wir haben. Während eine Linie der besten Anpassung technisch ein stärkerer Kandidat für diese Annahme wäre, hat die Schaffung von Grenzen zur Reduzierung der Anzahl der Ausgaben den gleichen Effekt, da Korrekturbrillen sowieso in inkrementellen einheitlichen Werten erhältlich sind. Dies wird in späteren Schritten erklärt.

Schritt 8: Anzeigen des Rezepts des Benutzers in einem Diagramm

Verwenden des folgenden Codes:

• Abbildung;
• plot(GivenPrescription, MagArray, '-g')
• festhalten
• plot(Rezept, Vergrößerung, 'bp')
• warte ab
• Netz
• legend('Daten', 'Interpolierte Punkte', 'Ort', 'NW')

Wir können ein Diagramm zeichnen, das die Vergrößerungsverhältnisse gegenüber der gegebenen Verschreibung mit einer grünen Linie und die gefundenen Daten unserer berechneten Vergrößerung gegenüber unserer interpolierten Verschreibung mit einem blauen Stern zeigt. Dann beschriftet die Legende den Titel, die X-Achse und die Y-Achse und platziert die Legende in der oberen linken Ecke.

Schritt 9: Grenzen Sie Ihr Rezept ein

Der folgende Code wird verwendet, um die Rundung für die Verschreibung zu erzeugen:

• wenn Rezept <= 1,125

  Berechnetes Rezept = '1.0';

• elseif Rezept <= 1.375

  Berechnetes Rezept = '1,25';

• elseif Rezept <= 1,625

  Berechnetes Rezept = '1,5';

• elseif Rezept <= 1.875

  Berechnetes Rezept = '1.75';

• elseif Rezept <= 2.25

  Berechnetes Rezept = '2.0';

• elseif Rezept <= 2.625

  Berechnetes Rezept = '2,5';

• elseif Rezept <= 3

  Berechnetes Rezept = '2,75';

• elseif Rezept <= 3.375

  Berechnetes Rezept = '3,25';

• anders

  CalculatedPrescription = 'unbekannt';

• Ende

Die durch die Interpolation ermittelte Verschreibung spiegelt nicht unbedingt die tatsächliche Verschreibung wider – das liegt daran, dass es aufgrund menschlicher Fehler immer zu leichten Abweichungen bei der Analyse des Fotos kommen wird. Daher benötigen wir diesen Schritt, um die tatsächliche Verschreibung zu klassifizieren.

Die Verschreibungen, die normalerweise verabreicht werden, beginnen bei 1,0 Dioptrien und erhöhen sich um 0,25 in ihren Verschreibungen. Nach der Berechnung der Verschreibung möchten wir also die Verschreibung bestimmen, die den Bedürfnissen des Benutzers am besten entspricht. Nach der Berechnung der Verschreibung führen wir sie durch die gegebenen If-Anweisungen, um ihren Wert zu überprüfen und festzustellen, welche Verschreibung erforderlich ist. Alles unter oder gleich 1,125, dann ist die Verschreibung 1,0. Alles unter oder gleich 1,375 beträgt die Verschreibung 1,25. Alles unter oder gleich 1,625 beträgt die Verschreibung 1,5. Alles unter oder gleich 1,845 beträgt die Verschreibung 1,75. Und so weiter.

Die Werte steigen, da wir prüfen, ob die Werte kleiner sind als. Wenn wir die Werte verringern würden, würde die erste if-Anweisung die erste if-Anweisung die ganze Zeit lesen. Wenn die Verschreibung die kleinste ist, möchten wir, dass sie sofort als die kleinste erkannt wird. Deshalb haben wir mit dem kleinsten Wert begonnen. Alles, was höher als der höchste Wert ist, bedeutet, dass die Verschreibung nicht im Bereich unserer Daten liegt, sodass die Zeichenfolge „Unbekannt“angezeigt wird.