Bioimpedanzanalyse (BIA) mit dem AD5933 - Gunook

2024 Autor: John Day | [email protected]. Zuletzt bearbeitet: 2024-01-30 07:18

Ich war daran interessiert, einen Bio-Impedanz-Analysator für Körperzusammensetzungsmessungen herzustellen, und meine zufälligen Suchen fanden immer wieder ein Design aus der Klasse für biomedizinische Instrumente von 2015 an der Vanderbilt University. Ich habe das Design durchgearbeitet und etwas verbessert. Ich möchte meine Erkenntnisse mit Ihnen teilen. Nehmen Sie aus dieser "Anleitung" mit, was Sie verwenden können, wenn etwas nicht klar ist, schlagen Sie bitte Verbesserungen vor. Vielleicht schreibe ich eines Tages meinen Gedanken in einer zusammenhängenderen Form auf, aber im Moment hoffe ich, dass Sie alles verwenden können, was Sie hier sehen. (Wenn Sie denken, dass Sie dies aufschreiben und verbessern können, sind Sie willkommen)

Teddy

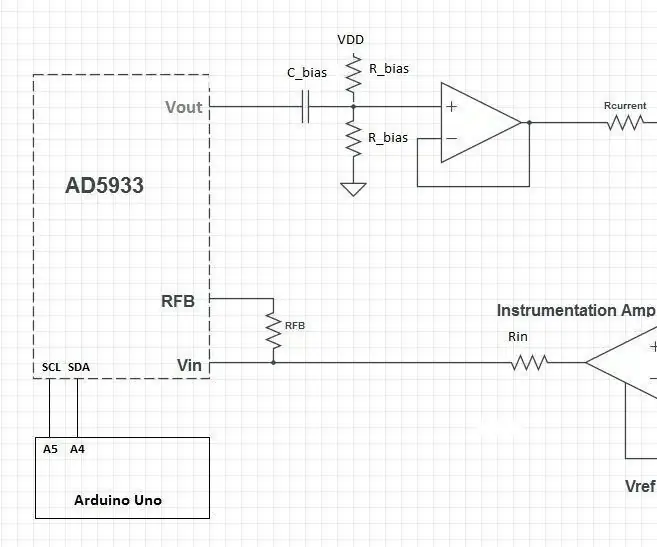
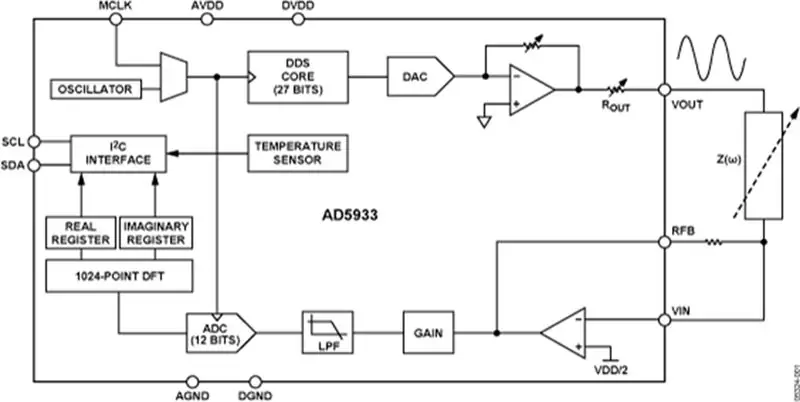
Dieses Design besteht aus dem AD5933-Chip und einem benutzerdefinierten analogen Front-End (AFE), um den AD5933 mit dem Gehäuse zu verbinden. Der AD5933 führt dann die Messung durch und die Ergebnisse können dann von einem Mikrocontroller (z. B. einem Arduino) verarbeitet werden.

Wenn Sie den Arduino als Stromversorgung verwenden möchten, stellen Sie sicher, dass die Operations- und Instrumentenverstärker (Op-Amps und In-Amps) sogenannte "Single Supply"-Spannungen unterstützen und über Rail-to-Rail-Spezifikationen verfügen.

(Im Folgenden verwende ich eine Stromversorgung (von einem Arduino) von 5V und die Einstellung von Range 1 auf dem AD5933.)

Schritt 1: Die Re-Bias-Phase

Der erste Teil des AFE ist eine Re-Bias-Stufe. Das Ausgangsspannungssignal ist nicht in der Mitte des Versorgungsspannungsbereichs (VDD/2) zentriert. Dies wird korrigiert, indem ein Kondensator verwendet wird, um den DC-Anteil des Signals zu blockieren und ihn durch einen Spannungsteiler zu senden, um dem Signal einen DC-Offset hinzuzufügen.

Die beiden Re-Bias-Widerstände können jeden Wert haben, solange sie gleich sind. Der spezifische Wert der Kappe ist ebenfalls nicht wichtig.

Die Re-Bias-Stufe arbeitet wie ein Hochpassfilter und hat daher eine Grenzfrequenz:

f_c = 1 / (2*pi * (0.5*R) * C)

Stellen Sie sicher, dass die Grenzfrequenz einige Jahrzehnte unter der minimalen Frequenz liegt, die Sie verwenden möchten. Wenn Sie in Ihrer Anwendung 1 kHz verwenden möchten, sollten Sie sich für Obergrenzen und Widerstandswerte entscheiden, die Ihnen eine Grenzfrequenz in der Größenordnung von 1-10 Hz ergeben.

Der letzte Teil dieser Stufe ist ein Operationsverstärker, der als Spannungsfolger eingerichtet ist. Dies soll sicherstellen, dass die Widerstandswerte die nächste Stufe nicht stören

Schritt 2: Strommesswiderstand

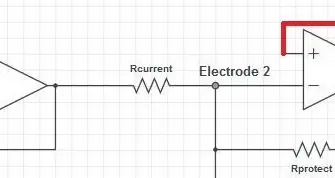
Der erste Teil der nächsten Stufe ist der Strommesswiderstand. Der Strom durch diesen Widerstand ist der gleiche Strom, den der Verstärker versucht, durch den Körper aufrechtzuerhalten. Stellen Sie sicher, dass der Strom den Sicherheitsstandards IEC6060-1 entspricht*:

Unterhalb von Frequenzen von 1 kHz dürfen maximal 10 Mikroampere (RMS) durch den Körper geleitet werden. Bei Frequenzen über 1 kHz ergibt die folgende Gleichung den maximal zulässigen Strom:

Max. Wechselstrom < (Mindestfrequenz in kHz) * 10 Mikroampere (RMS)

Die Beziehung zwischen der Spitzenamplitude eines AC-Signals und seinem RMS-Wert ist: Peak = sqrt(2) * RMS. (10 Mikroampere RMS entsprechen 14 Mikroampere Spitzenamplitude)

Unter Verwendung des Ohmschen Gesetzes für den Widerstand können wir den Widerstandswert berechnen, der dem Sicherheitsstandard entspricht. Wir verwenden die Erregerspannung des AD5933 und den maximalen Stromwert:

U = R * I => R = U / I

Z. B. mit der Einstellung von Bereich 1 Upeak = 3V / 2 = 1,5V (oder 1V @3,3V)

Mit dem 14 microAmp Spitzenwert von oben erhalte ich einen Widerstandswert von mindestens 107kOhm

Verweise:

* Analog Devices: "Bio-Impedance Circuit Design for Body Worn Systems"

Schritt 3: Der Transkonduktanzverstärker

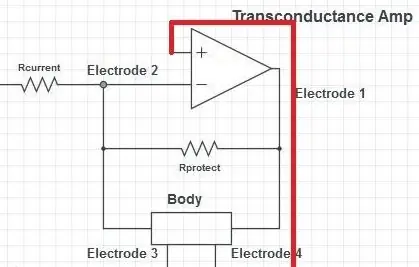
Nach dem Strommesswiderstand befindet sich ein Operationsverstärker in einer Konfiguration mit negativer Rückkopplung. Dies ist ein sogenanntes Load-in-the-Loop-Setup. Der positive Eingangsanschluss des Operationsverstärkers ist mit einer VDD/2-Spannung verbunden. Der Operationsverstärker versucht nun, seinen Ausgang in die entgegengesetzte Richtung zum Anregungssignal einzustellen, so dass die Spannung am negativen Anschluss gleich VDD/2 ist. Dies erzeugt ein wippendes Potential, das den Strom durch den Körper drückt und zieht.

Der vom Minuspol des Operationsverstärkers gezogene Strom ist praktisch Null. Der gesamte Strom durch den Strommesswiderstand muss daher durch den Körper fließen. Dies ist der Mechanismus, der dieses Setup zu einem Transkonduktanzverstärker macht (auch spannungsgesteuerte Stromquelle, VCCS genannt).

Der Operationsverstärker kann den Strom nur aufrechterhalten, wenn die Impedanz des Körpers nicht zu hoch ist. Andernfalls würde der Operationsverstärkerausgang bei der Versorgungsspannung (0 oder 5 V) nur das Maximum erreichen. Die maximal einzuhaltende Spannungsspanne beträgt VDD/2 + Upeak (2,5+1,5V = 4V @ 5V Versorgung). Die Spannungsmargen des Operationsverstärkers sollten von diesem Wert abgezogen werden, aber wenn der Operationsverstärker Rail-to-Rail-Spezifikationen hat, wäre dies nur ein kleiner Betrag. Die maximale Impedanz, die der Operationsverstärker ansteuern kann, beträgt daher:

Z < (VDD/2 + Upeak) / Imax

(In meinem Setup Z < 4V / 14 microAmps = 285 kOhm, der Wunsch ist ausreichend, den Impedanzbereich des Körpers abzudecken)

Der Schutzwiderstand hat einen sehr großen Wert (1-1,5 MOhm) im Vergleich zum Körper (ca. 100 kOhm) und zieht bei allen normalen Operationen keinen merklichen Strom und die Impedanz der Parallelschaltung wird von der Impedanz des Körpers dominiert. Wenn die Impedanz des Körpers ansteigen sollte (z. B. Pads lösen sich), kann der Strom durch den Widerstand fließen und das Maximieren des Operationsverstärkers würde keine unangenehmen Spannungen in den Pads erzeugen.

Schritt 4: Der Instrumentierungsverstärker

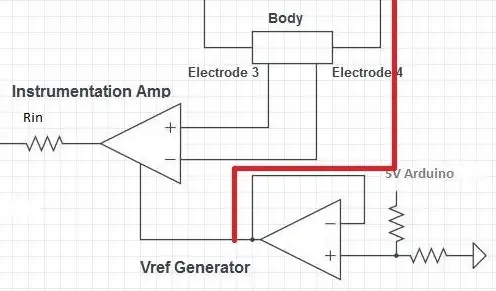
Die nächste Stufe ist der Instrumentenverstärker (In-Amp), der die Spannung am Körper misst. Die Spannung am Körper oszilliert um 0 V, aber der AD5933 benötigt eine Eingangsspannung im positiven Bereich. Der Eingangsverstärker fügt dem gemessenen Spannungssignal daher einen DC-Offset von VDD/2 hinzu.

Die VDD/2-Referenz wird von einem Spannungsteiler erzeugt. Jeder beliebige Widerstandswert kann verwendet werden, solange sie gleich sind. Der Spannungsteiler ist durch einen Spannungsfolger von der Impedanz der restlichen Schaltung getrennt. Der Ausgang des Spannungsfolgers kann dann sowohl an den Eingangsverstärker als auch an den Transkonduktanzverstärker weitergeleitet werden.

Schritt 5: Die Eingangsstufe und Kalibrierung

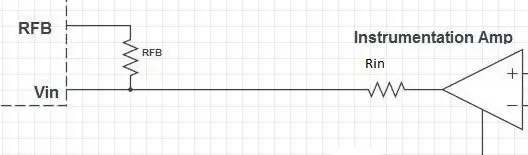
Die Eingangsstufe des AD5933 enthält einen Operationsverstärker in negativer Rückkopplungskonfiguration. Es gibt zwei Widerstände: einen in Reihe (Rin) und einen parallel (RFB). Die Verstärkung des Operationsverstärkers ist gegeben durch

A = - RFB / Rin

Die Verstärkungen des Eingangs-Operationsverstärkers und des Eingangsverstärkers (und des PGA) müssen sicherstellen, dass das Signal, das in den ADC des AD5933 eingeht, immer innerhalb von 0 V und VDD liegt.

(Ich verwende einen Verstärkungsfaktor von Eins und Widerstandswerte, die ungefähr A = 0,5 ergeben)

Im AD5933 wandelt der ADC das Spannungssignal in ein digitales Signal um. Der Spannungsbereich von 0V bis VDD wird in den digitalen Bereich 0-128 (2^7) umgewandelt. (Die Dokumentation ist diesbezüglich nicht klar, aber eine genaue Untersuchung der Plots in [1] und einige Experimente meinerseits bestätigen dies.)

Innerhalb des DFT-Moduls erfolgt eine weitere Skalierung von 256 (1024/4, siehe [1]), bevor das Ergebnis im Real- und Imaginärregister gespeichert wird.

Indem man dem Spannungssignal durch das AFE in den ADC folgt und die zuvor erwähnten Skalierungsfaktoren verwendet, ist es möglich, den Verstärkungsfaktor zu schätzen:

g = (VDD * Rcurrent * Rin) / (256 * PGA * Upeak * RFB * 2^7)

Es kann noch eine Kalibrierung erforderlich sein. Berücksichtigen Sie daher einige Effekte, die nicht Teil dieses mathematischen Modells sind. (g = Z / mag, siehe unten)

Die Impedanz kann nun berechnet werden durch

Z = g * mag

mag = sqrt (real^2 + imaginär^2)

PA = arctan2(real, imaginär) - deltaPA

Die PA muss wahrscheinlich kalibriert werden, da es beim AD5933 eine systematische Phasenverschiebung als Funktion der Frequenz gibt. deltaPA wird wahrscheinlich eine lineare Funktion der Frequenz sein.

Der Widerstand und die Reaktanz können nun berechnet werden durch

R = Z * cos(PA)

X = Z * sin(PA)

Referenzen:[1] Leonid Matsiev, "Improving Performance and Versatility of Systems Based on Single-Frequency DFT Detectors Like AD5933", Electronics 2015, 4, 1-34; doi:10.3390/electronics4010001

Schritt 6: Advanced Stuff: Spectral Leakage (DC)

Das Signal, das wir in den AD5933 eingeben, ist eine Spannung/Strom als Funktion der Zeit, aber unser Hauptinteresse gilt der Impedanz als Funktion der Frequenz. Um zwischen Zeitbereich und Frequenzbereich zu konvertieren, müssen wir die Fourier-Transformation des Zeitbereichssignals nehmen. Der AD5933 verfügt über ein eingebautes Modul zur diskreten Fourier-Transformation (DFT). Bei niedrigen Frequenzen (unter etwa 10 kHz) wird der DFT-Aufbau durch Aliasing und spektrale Lecks beeinflusst. In [1] geht er durch die Mathematik, wie man die spektrale Leckage korrigiert. Der Kern davon besteht darin, fünf (plus zwei) Konstanten für jeden Frequenzschritt im Sweep zu berechnen. Dies kann leicht z. B. durch den Arduino in der Software.

Der Leckstrom tritt in zwei Formen auf: ein Gleichstromverlust, der von Natur aus additiv ist, und ein Wechselstromverlust, der multiplikativer Natur ist.

Der DC-Leckstrom rührt daher, dass das Spannungssignal am ADC nicht um 0 V, sondern um VDD/2 schwingt. Ein DC-Pegel von VDD/2 sollte einem digitalen DC-Wert von ca. 64 entsprechen (bezeichnet als Delta in [1]).

Die Schritte zum Korrigieren der spektralen DC-Leckage:

1) Berechnen Sie den Hüllkurvenfaktor E für die aktuelle Frequenz.

2) Berechnen Sie die beiden Verstärkungsfaktoren GI (real) und GQ (imaginär)

3) Subtrahiere Delta * GI vom Wert des reellen Registers und Delta * GQ vom Wert des imaginären Registers

Verweise:

[1] Leonid Matsiev, „Verbesserung der Leistung und Vielseitigkeit von Systemen basierend auf

Einzelfrequenz-DFT-Detektoren wie AD5933 , Electronics 2015, 4, 1-34; doi:10.3390/electronics4010001

[2] Konrad Chabowski, Tomasz Piasecki, Andrzej Dzierka, Karol Nitsch, "Simple Wide Frequency Range Impedance Meter Based on AD5933 Integrated Circuit", Metrol. Maße Syst., Vol. 2, No. XXII (2015), Nr. 1, S. 13–24.

Schritt 7: Advanced Stuff: Spectral Leakage (AC)

Wie der DC-Leckstrom kann der AC-Leckstrom mathematisch korrigiert werden. In [1] werden Widerstand und Reaktanz als A*cos(phi) bzw. A*sin(phi) bezeichnet, wobei A dem Betrag der Impedanz und phi dem Phasenwinkel (PA) entspricht.

Die Schritte zum Korrigieren des spektralen Wechselstromlecks:

1) Berechnen Sie den Hüllkurvenfaktor E (nicht der gleiche wie bei DC) für die aktuelle Frequenz.

2) Berechnen Sie die drei Faktoren a, b und d. (ungefähre Werte bei höheren Frequenzen: a = d = 256 und b = 0)

3) Widerstand (Acos(phi)) und Reaktanz (Asin(phi)) können jetzt in digitalen Einheiten berechnet werden

Referenzen:[1] Leonid Matsiev, "Improving Performance and Versatility of Systems Based on Single-Frequency DFT Detectors Like AD5933", Electronics 2015, 4, 1-34; doi:10.3390/electronics4010001

[2] Konrad Chabowski, Tomasz Piasecki, Andrzej Dzierka, Karol Nitsch, "Simple Wide Frequency Range Impedance Meter Based on AD5933 Integrated Circuit", Metrol. Maße Syst., Vol. 2, No. XXII (2015), Nr. 1, S. 13–24.

Schritt 8: Advanced Stuff: der theoretische Gain-Faktor

Aufgrund der mathematischen Modellierung der DFT sollte es auch möglich sein, das gesamte AFE mathematisch zu modellieren. Mathematisch kann das Spannungssignal durch eine Sinusfunktion mit einer gegebenen festen Frequenz, einem DC-Offset und einer AC-Schwingung mit einer Spitzenamplitude beschrieben werden. Die Frequenz ändert sich während eines Frequenzschritts nicht. Da der Verstärkungsfaktor nur die Größe der Impedanz und nicht den PA ändert, werden wir uns hier nicht mit einer im Signal induzierten Phasenverschiebung befassen.

Hier ist eine kurze Zusammenfassung des Spannungssignals, wie es sich durch das AFE ausbreitet:

1) Nach der Re-Bias-Stufe beträgt die AC-Amplitude immer noch Upeak = 1,5 V (1 V @ VDD = 3,3 V) und der DC-Offcet wurde auf VDD/2 geändert.

2) Im Strommesswiderstand ist die Spannung immer noch die gleiche wie in der vorherigen Stufe …

3) … aber aufgrund der Wippspannung des Operationsverstärkers haben die AC-Schwingungen eine Größe von Z*Upeak/Rcurrent. (Der DC-Offset wird durch die Operationsverstärker-Referenzspannung von VDD/2 - dem Drehpunkt der Wippe - aufgehoben und wird in diesem Teil der Schaltung zu einer virtuellen Masse.)

4) Der Unity In-Amp fügt den DC-Offset von VDD/2 wieder ein und leitet das Signal an die Eingangsstufe des AD5933. weiter

5) Der Operationsverstärker in der Eingangsstufe hat eine Verstärkung von A=-RFB/Rin und die AC-Amplitude wird daher (Z*Upeak/Rcurrent)*(RFB/Rin)

6) Kurz vor dem ADC befindet sich ein programmierbarer Verstärkungsverstärker (PGA) mit zwei Einstellungen einer Verstärkung von 1 oder 5. Das Spannungssignal am ADC wird daher zu: PGA*(Z*Upeak/Rcurrent)*(RFB/Rin)

Der ADC wandelt das v(t)-Signal in ein digitales Signal x(t) = u(t) / VDD * 2^7 mit einer Genauigkeit von 12 Bit um.

Die Größe A ist durch den Verstärkungsfaktor k mit der Impedanz Z verbunden, da A = k * Z und hat einen ungefähren Wert von k = PGA * Upeak * RFB * 2^7 / (VDD * Rcurrent * Rin).

Wenn Sie stattdessen mit Gain-Faktor arbeiten möchten, g = 1 / k und Z = g * A.

Schritt 9: Advanced Stuff: die PA-Shift

In [2] finden sie eine systematische Verschiebung der PA als Funktion der Frequenz. Dies liegt an einer Zeitverzögerung zwischen dem DAC, wo das Anregungssignal erzeugt wird, und der DFT, wo das ankommende Signal mit dem abgehenden Signal gefaltet werden muss.

Die Verschiebung wird durch die Anzahl der Taktzyklen charakterisiert, die das Signal zwischen dem DAC und der DFT intern im AD5933 verzögert.

Referenzen:[1] Leonid Matsiev, "Improving Performance and Versatility of Systems Based on Single-Frequency DFT Detectors Like AD5933", Electronics 2015, 4, 1-34; doi:10.3390/electronics4010001

[2] Konrad Chabowski, Tomasz Piasecki, Andrzej Dzierka, Karol Nitsch, "Simple Wide Frequency Range Impedance Meter Based on AD5933 Integrated Circuit", Metrol. Maße Syst., Vol. 2, No. XXII (2015), Nr. 1, S. 13–24.