☠WEEDINATOR☠ Teil 4: Differentiallenkungsgeometriecode - Gunook

2024 Autor: John Day | [email protected]. Zuletzt bearbeitet: 2024-01-30 07:21

Wenn Sie die Zeit haben, sich das obige Video anzusehen, werden Sie feststellen, dass es ab und zu seltsame Geräusche gibt, die durch das Abwürgen der Motoren an der Lenkung verursacht werden, wenn der WEEDINATOR eine 3-Punkt-Kurve fährt. Die Motoren klemmen im Wesentlichen gegeneinander, da der Wenderadius von innen nach außen unterschiedlich ist und die Distanz, die das Rad zurücklegt, je nach Grad der Drehung unterschiedlich ist.

Die Geometrie der Kurve kann durch Skizzieren von etwa 8 Permutationen der Kurve herausgearbeitet werden, wobei Beispiele für das Drehen in verschiedenen Winkeln auf dem inneren Rad von 0 (keine Drehung) bis 90 (Vollsperrung) Grad angegeben werden. Klingt kompliziert?

Die meisten Roboter mit kleinen Rädern versuchen nicht, eine ausgeklügelte Lenkung zu haben und verlassen sich sehr effektiv darauf, einfach die relative Geschwindigkeit der Motoren auf jeder Seite des Fahrzeugs zu ändern, was ziemlich ähnlich ist wie bei einem Kettenbagger oder Panzer funktioniert. Dies ist großartig, wenn Sie über ein kratergefülltes Kriegsgebiet stürmen und auf alles schießen, was sich bewegt, aber in einer ruhigen landwirtschaftlichen Umgebung ist es wichtig, den Boden und den Boden so wenig wie möglich zu beschädigen, damit das Schleifen der Räder vor und zurück gegeneinander ist nicht angemessen!

Die meisten Autos und Traktoren haben ein sehr nützliches Gerät namens "Differential", außer den Autos, die Sie in alten amerikanischen Filmen sehen, wo Sie jedes Mal, wenn sie um eine Ecke fahren, die Reifen wie verrückt kreischen hören können. Bauen Amerikaner noch solche Autos? Mit dem WEEDINATOR können wir Differenzial in die Antriebsmotoren programmieren, indem wir die Formel für die relativen Geschwindigkeiten und Winkel der Räder bei einem bestimmten Drehwinkel berechnen. Klingt immer noch kompliziert?

Hier ist ein kurzes Beispiel:

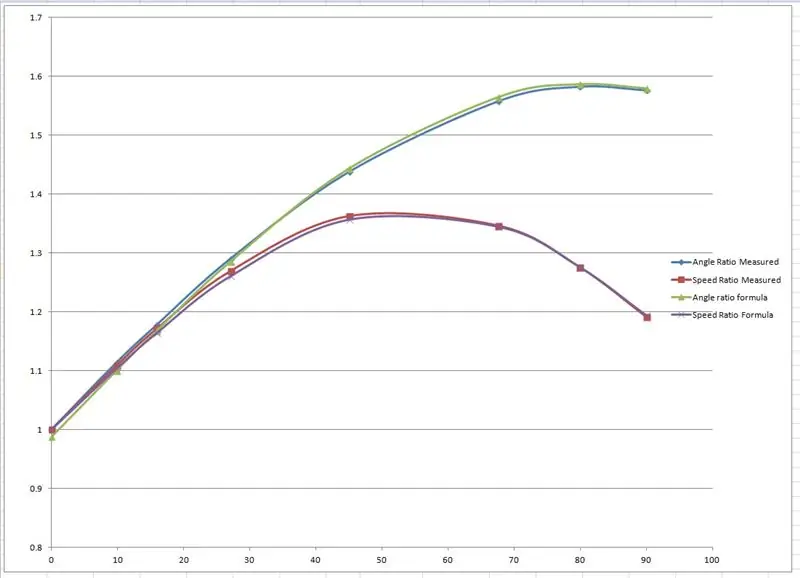
Wenn der WEEDINATOR eine Kurve fährt und sein Innenrad bei 45 Grad hat, ist das Außenrad NICHT 45 Grad, es sind eher 30 Grad. Außerdem kann sich das kurveninnere Rad mit 1 km/h drehen, aber das kurvenäußere Rad ist deutlich schneller, etwa 1,35 km/h.

Schritt 1: Geometrie-Setup

Zu Beginn werden einige Grundannahmen gemacht:

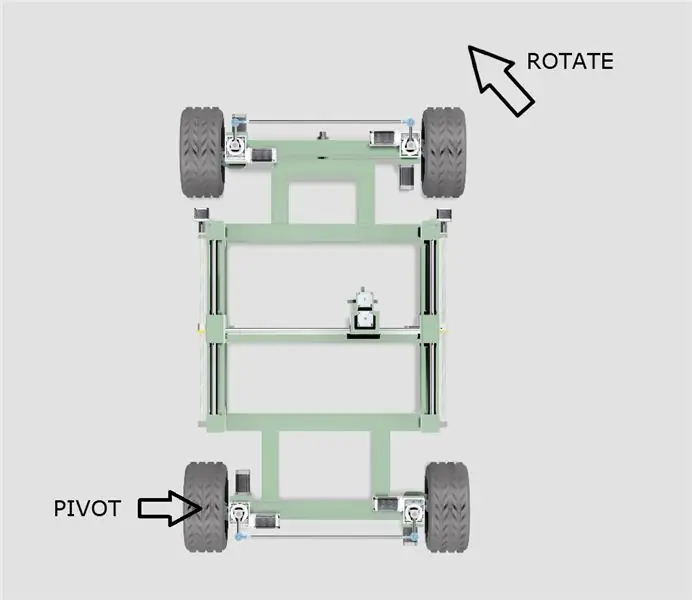
• Das Chassis schwenkt um eines der Hinterräder, wie in der Abbildung oben gezeigt.
• Der effektive Mittelpunkt des Schwenkkreises bewegt sich je nach Drehwinkel entlang einer Linie, die von den Mittelpunkten der beiden Hinterräder ausgeht.
• Die Geometrie nimmt die Form einer Sinuskurve an.

Schritt 2: Skalierte Zeichnungen von Radwinkeln und Radien

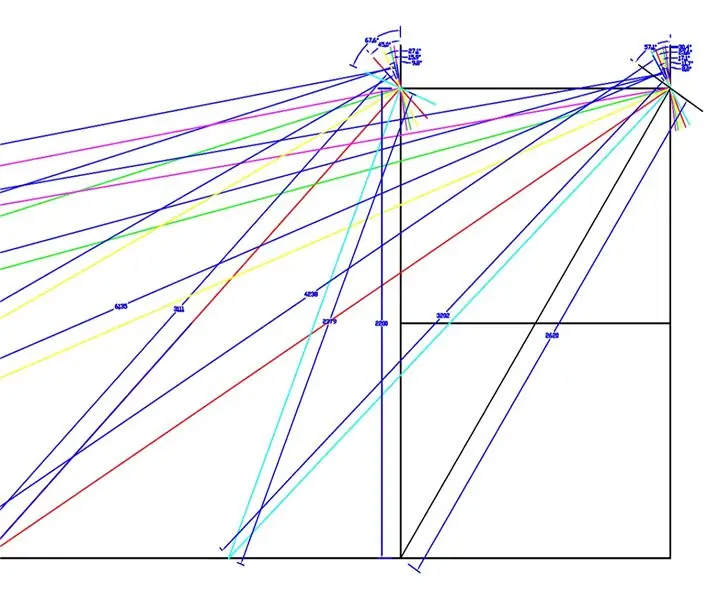
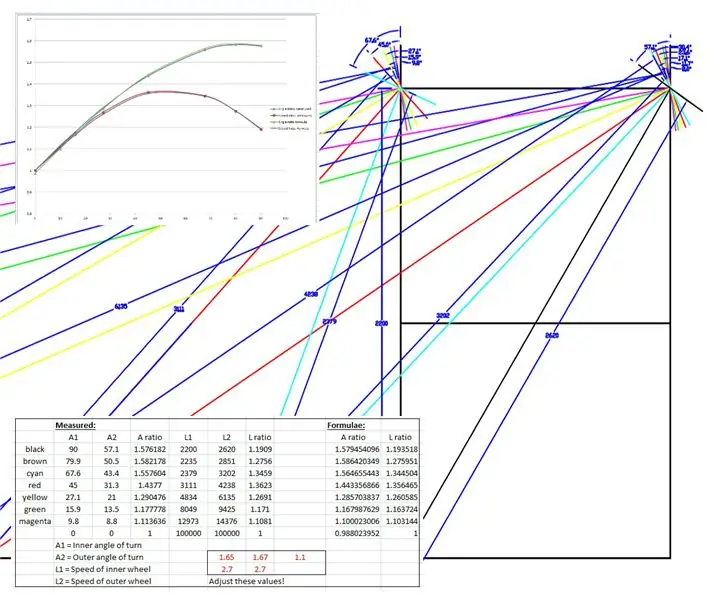
Es wurde eine maßstabsgetreue Zeichnung der WEEDINATOR-Vorderräder und des Chassis mit 8 verschiedenen Permutationen des Innenradwinkels zwischen 0 und 90 Grad erstellt und die jeweiligen Wendezentren wurden wie in den obigen Zeichnungen gezeigt abgebildet.

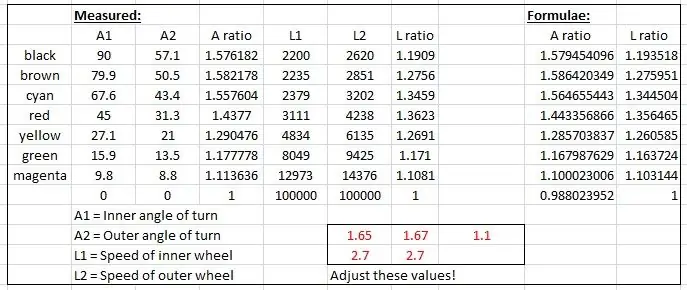
Die effektiven Radien wurden aus der Zeichnung gemessen und in einem Diagramm in Microsoft Excel aufgetragen.

Es wurden zwei Diagramme erstellt, eines für das Verhältnis der linken und rechten Vorderradachsen und ein weiteres für das Verhältnis der beiden Radien für jeden einzelnen Einschlagwinkel.

Ich habe dann einige Formeln "gefälscht", um die empirischen Ergebnisse basierend auf einer Sinuskurve nachzuahmen. Einer der Fudges sieht so aus:

speedRatio= (sin(inner*1,65*pi/180)+2,7)/2,7; // inner ist der innere Drehwinkel.

Die Kurven wurden gefälscht, indem die rot angezeigten Werte in der Excel-Datei geändert wurden, bis die Kurven zusammenpassten.

Schritt 3: Codieren der Formeln

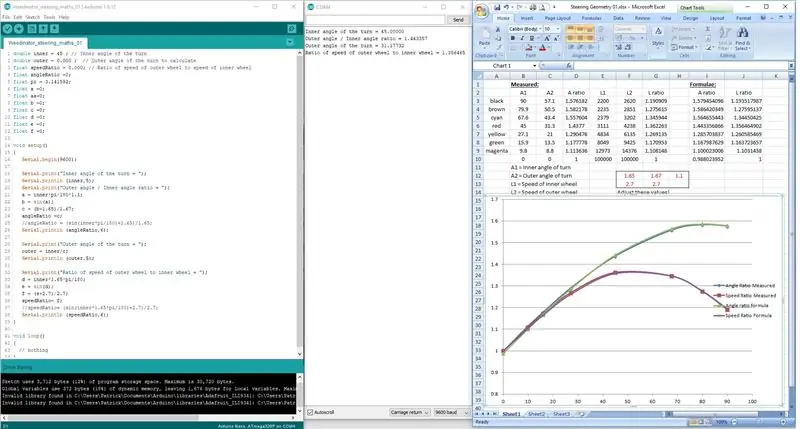
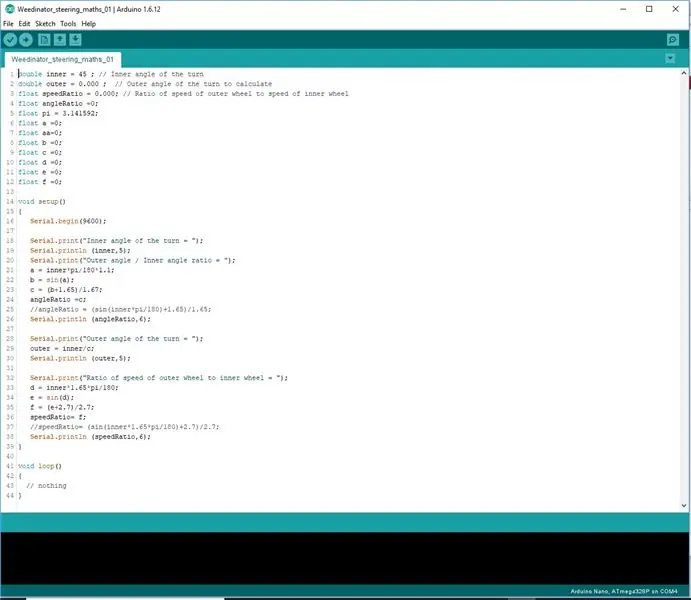
Anstatt zu versuchen, die Formeln in einer Zeile zu codieren, wurden sie in 3 Stufen unterteilt, damit der Arduino die Mathematik richtig verarbeiten kann.

Die Ergebnisse werden im Display der seriellen Schnittstelle angezeigt und mit den Messergebnissen auf der Maßzeichnung verglichen.