
Inhaltsverzeichnis:
- Autor John Day day@howwhatproduce.com.
- Public 2024-01-30 07:23.
- Zuletzt bearbeitet 2025-01-23 12:53.
Dieses instructable deckt einige der grundlegendsten Funktionen von Matlab ab. Sie werden lernen, wie Sie Matlab intern eine periodische Funktion ausführen und plotten lassen und wie Sie stattdessen dieselbe periodische Funktion aus einer Excel-Datei ziehen und plotten. Diese Funktionen gehören zu den grundlegendsten und am häufigsten verwendeten in Matlab. Dieses anweisbare richtet sich an diejenigen von Ihnen, die Matlab noch nie zuvor verwendet haben und nur einige einfache Aufgaben damit ausführen müssen. Der in jedem Bild hervorgehobene Code ist als Kommentar enthalten, sodass Sie den Code kopieren und einfügen können. Nehmen Sie diesen Code gerne und passen Sie ihn an Ihre Anwendung an.
Schritt 1: Matlab starten
Der erste Schritt besteht darin, Matlab zum Laufen zu bringen, damit wir damit beginnen können. Wenn Sie Matlab zum ersten Mal starten, sollte es wie im Screenshot unten aussehen. Der erste Schritt besteht darin, ein Verzeichnis zuzuweisen, von dem aus Matlab arbeiten kann. Hier zieht das Programm alle Dateien und hier sollten Sie alle Ihre Matlab-Arbeiten speichern. Nachdem Sie einen neuen Ordner erstellt haben, klicken Sie oben rechts auf dem Bildschirm auf "…", wie im zweiten Bild hervorgehoben. Dadurch wird ein Suchfeld geöffnet, wie im dritten Bild zu sehen. Suchen Sie den neuen Ordner, den Sie auf Ihrem Computer erstellt haben, und wählen Sie ihn aus. In diesem Beispiel heißt die Datei "370" und befindet sich auf dem Desktop.
Schritt 2: Erstellen einer M-Datei
Jetzt müssen wir eine neue M-Datei erstellen. Eine M-Datei funktioniert genauso wie die direkte Eingabe von Code in Matlab, aber Sie können den Code speichern, ändern und wiederholt ausführen. Wenn Sie Code direkt in Matlab eingeben, geben Sie jede Codezeile einzeln ein. In eine M-Datei schreiben Sie Ihren gesamten Code und führen ihn dann auf einmal aus. Um eine neue M-Datei zu öffnen, klicken Sie auf Datei. Platzieren Sie Ihren Cursor auf "Neu" und klicken Sie dann auf "Leere M-Datei", wie im ersten Bild gezeigt. Was sich öffnet, sollte wie das zweite Bild aussehen. Da dieser Code wiederholt ausgeführt werden kann, ist es eine gute Idee, alles zu schließen und alle Variablen zu löschen, bevor er jedes Mal ausgeführt wird. Dies wird durch zwei Codezeilen erreicht:close allclear allWie im dritten Bild zu sehen ist, wird sichergestellt, dass alles gelöscht und geschlossen ist.
Schritt 3: Erstellen eines Zeitvektors
Als erstes erstellen wir einen Funktionsgraphen in Matlab. Der erste Schritt besteht darin, die unabhängige Variable zu erstellen. In diesem Fall nennen wir es "t" für Zeit. Die Methode, mit der wir diese Variable erstellen, besteht darin, einen Vektor zu erstellen. Ein Vektor ist im Grunde eine Reihe von Zahlen. 1, 2, 3, 4 wäre beispielsweise ein kurzer Vektor. Der Code zum Erstellen dieses Vektors lautet:t=0.1:0.01:10;Die erste Zahl, 0.1, bezieht sich auf den Startpunkt. Die zweite Zahl, die 0,01, bezieht sich auf die Schrittweite. Die dritte Zahl, 10, bezieht sich auf den Endpunkt. Dieser Vektor entspricht also 0.1, 0.11, 0.12 … bis hin zu 10. Um zu sehen, ob das Erstellen des Vektors funktioniert hat, klicken Sie auf die im zweiten Bild hervorgehobene grüne Schaltfläche Ausführen. Dadurch wird das Programm ausgeführt. Um unseren Vektor zu sehen, gehen Sie zum Hauptfenster von Matlab. Klicken Sie auf Desktop, fahren Sie dann mit der Maus über das Desktop-Layout und klicken Sie dann auf Standard, wie im dritten Bild dargestellt. Jetzt sollte Ihr Bildschirm wie das vierte Bild aussehen. Rechts sehen Sie unsere neu erstellte Variable t. Doppelklicken Sie darauf und wie im fünften Bild sehen Sie die erstellte Zahlenreihe.
Schritt 4: Ausführen und grafische Darstellung einer Funktion
Jetzt werden wir eine in Matlab erstellte Funktion grafisch darstellen. Der erste Schritt besteht darin, die Funktion zu erstellen. Dies ist so einfach wie das Ausschreiben der gewünschten mathematischen Funktion. Ein Beispiel ist im ersten Bild gezeigt. Der für diese Funktion verwendete Code lautet:y=sin(t)+4*cos(5.*t).^2;Der Zeitraum vor der Multiplikation im Kosinus und vor dem Quadrat des Kosinus weist Matlab an, diese Funktionen auszuführen einfach auf die Wertigkeiten des Zeitvektors, nicht den Zeitvektor als Matrix zu behandeln und zu versuchen, Matrixfunktionen darauf auszuführen. Der nächste Schritt besteht darin, die Figur selbst zu erstellen. Dies wird mit dem in der zweiten Abbildung gezeigten Code erreicht. Die Reihenfolge der Variablen im Plot-Befehl ist sehr wichtig, also stellen Sie sicher, dass Sie Ihren Code so einrichten, wie er unten eingerichtet ist.figureh=axes('fontsize', 14);plot(t, y, 'linewidth, 2) xlabel('Time(s)')ylabel('Y Value')Title('Y Value vs Time')grid onKlicken Sie abschließend noch einmal auf den grünen Laufpfeil und die Zahl sollte wie im dritten Bild erscheinen.
Schritt 5: Daten aus Excel abrufen
Wir erstellen jetzt das gleiche Diagramm wie zuvor, aber indem wir die Funktionsdaten aus einer Excel-Tabelle importieren. Das erste Bild ist ein Screenshot der Excel-Tabelle, die verwendet wird. Es sind genau die gleichen Datenpunkte, die in den vorherigen Schritten in Matlab erstellt wurden, nur in Excel. Um zu beginnen, können wir den Code löschen, der unseren Zeitvektor und den Code für unsere Funktion aus den vorherigen Schritten erstellt. Ihr Code sollte jetzt wie das zweite Bild aussehen. Fügen Sie den Code wie im oberen roten Feld des dritten Bildes gezeigt ein. Dies ist der Code zum Lesen der Excel-Datei. "A" bezieht sich auf eine Matrix, die alle Zahlen in der Tabelle enthält, und "B" enthält den gesamten Text aus der Tabelle. Die Variablen t und y werden aus der ersten und zweiten Spalte gezogen, wie im Code gezeigt.[A, B]=xlsread('excelexample.xlsx');t=A(:, 1);y=A(:, 2); Der Zahlencode kann auch geändert werden, wie im unteren roten Feld auf dem dritten Bild gezeigt. Dies wird tatsächlich den Diagrammtitel und die Achsenbeschriftungen aus der Tabelle ziehen und in Ihr Diagramm einfügen.xlabel(B(2))ylabel(B(3))Title(B(1))Zunächst das Programm ausführen erneut und Sie werden sehen, dass die gleiche Figur wie im letzten Bild angezeigt wird.
Schritt 6: Erstellen eines Specgrams
In diesem Schritt verwenden wir Matlab, um ein Specgram zu erstellen, indem wir eine WAV-Sounddatei lesen. Ein Specgram wird manchmal als "2,5D-Graphen" bezeichnet, weil es ein zweidimensionales Diagramm verwendet, das zusätzlich Farbe enthält, um die Amplitude anzuzeigen. Die Farbe liefert mehr Details als ein einfacher 2D-Graphen, aber nicht die Details eines 3D-Graphen, daher der Begriff "2.5D". Punkte, um die im Signal vorhandenen Frequenzen zu bestimmen. Für dieses anweisbare ist es nicht wichtig zu wissen, wie eine Fourier-Transformation funktioniert, wissen Sie nur, dass das Specgram darstellt, welche Frequenzen vorhanden sind und wie stark sie in Bezug auf die Zeit sind. Die Funktion zeichnet die Zeit auf der X-Achse und die Frequenz auf der Y-Achse auf. Die Stärke jeder Frequenz wird farblich angezeigt. In diesem Fall ist die WAV-Datei eine Tonaufnahme eines angeschlagenen Metallstücks, und dann werden die Schwingungen des Metalls als Ton aufgezeichnet. Mit dem Specgram können wir leicht die Resonanzfrequenz des Metallstücks bestimmen, da dies die Frequenz ist, die mit der Zeit am längsten anhält. fs]=wavread('flex4.wav');In diesem Fall ist flex4.wav der Titel unserer wav-Datei, die Variable x sind die Datenpunkte in der Datei und fs bezieht sich auf die Abtastfrequenz, geben Sie einfach den folgenden Code ein:specgram[x(:.1), 256, fs];Die 256 entspricht der Frequenz, mit der die FFT bei der Analyse der Daten durchgeführt wird. Matlab zerlegt die Sounddatei im Grunde in Stücke und nimmt eine FFT für jeden Abschnitt. Die 256 sagt ihm, wie groß jeder Abschnitt sein sollte. Die Details dazu sind nicht wichtig, und 256 ist ein sicherer Wert für die meisten Anwendungen. Wenn Sie nun den Code ausführen, sehen Sie ein Popup-Fenster wie im zweiten Bild zu sehen. Daraus ist leicht zu erkennen, dass die Resonanzfrequenz dem roten Peak in der unteren rechten Ecke der Abbildung entspricht. Dies ist der Peak, der in Bezug auf die Zeit am längsten anhält.
Empfohlen:
Erste Schritte mit Amara: 7 Schritte

Erste Schritte mit Amara: Amara ist ein kostenloser Untertitel-Editor, mit dem Sie ganz einfach Untertitel zu Videos hinzufügen können – vom Unterricht bis zum persönlichen Gebrauch. Diese Anweisungen helfen Ihnen, ein Amara-Konto einzurichten, damit Sie schnell und einfach Untertitel hinzufügen können
So programmieren und veröffentlichen Sie Matlab 2016b in Word (Anleitung für Anfänger): 4 Schritte

So codieren und veröffentlichen Sie Matlab 2016b in Word (Einsteigerhandbuch): Matlab ist ein leistungsstarkes Sprachprogramm, das zum Berechnen technischer Ergebnisse verwendet wird. Es hat die Fähigkeit, Visualisierungen, Berechnungen und Programmierung auf benutzerfreundliche Weise zu integrieren. Mit diesem Programm kann der Benutzer Probleme und Lösungen veröffentlichen
Erste Schritte mit der Heimautomatisierung: Home Assistant installieren: 3 Schritte
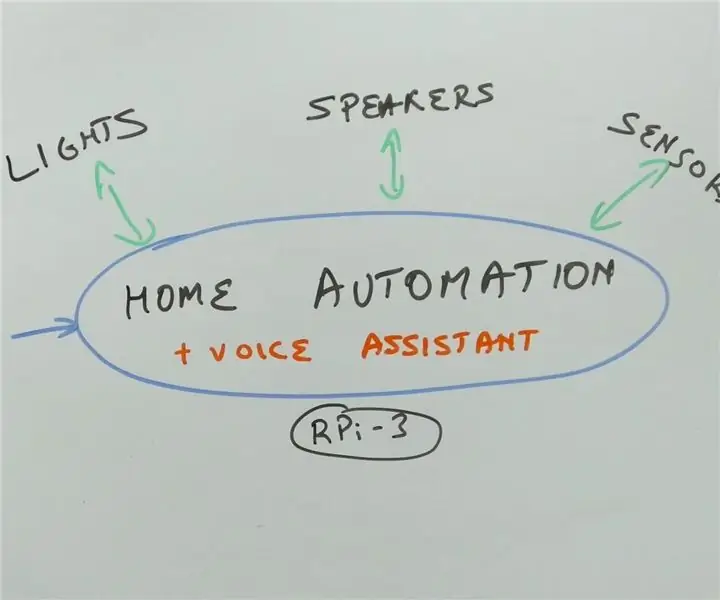
Erste Schritte mit der Hausautomation: Home Assistant installieren: Wir starten jetzt die Hausautomationsserie, in der wir ein Smart Home erstellen, das es uns ermöglicht, Dinge wie Licht, Lautsprecher, Sensoren usw. über einen zentralen Hub zusammen mit einem Sprachassistent. In diesem Beitrag erfahren Sie, wie Sie in
Programmiererweiterungen in MATLAB trainieren: 6 Schritte

Verbesserungen bei der Zugprogrammierung in MATLAB: Ziel: Das Ziel dieses programmierten Systems besteht darin, einen kleinen Arduino zu betrachten und die Codierung in größerem Maßstab anzuwenden, um möglicherweise bestimmte Sicherheitsfunktionen von Amtrak-Eisenbahnsystemen zu verbessern. Dazu haben wir einen Bodenfeuchtesensor hinzugefügt
Tutorial zum Abtasten analoger Signale - MATLAB: 8 Schritte

Tutorial zum Abtasten analoger Signale | MATLAB: In diesem Tutorial zeigen wir, was Sampling ist. und Wie man ein analoges Signal mit der MATLAB-Software abtastet
