Selbstausgleichender Roboter mit PID-Algorithmus (STM MC) - Gunook

2024 Autor: John Day | [email protected]. Zuletzt bearbeitet: 2024-01-30 07:20

In letzter Zeit wurde viel Arbeit im Selbstausgleich von Objekten geleistet. Das Konzept des Selbstausgleichs begann mit dem Ausgleich des umgekehrten Pendels. Dieses Konzept erstreckte sich auch auf das Design von Flugzeugen. In diesem Projekt haben wir ein kleines Modell eines selbstausgleichenden Roboters entworfen, der den PID-Algorithmus (Proportional, Integral, Derivative) verwendet. Seitdem ist diese Methode das neue Gesicht der industriellen Prozessleitsysteme. In diesem Bericht werden die Methoden beschrieben, die beim Selbstausgleich von Objekten beteiligt sind. Dieses Projekt wurde als Semesterprojekt durchgeführt, um den Zusammenhang von PID mit der Ezienz verschiedener industrieller Prozesse zu verstehen. Wir konzentrieren uns hier nur darauf, einen kurzen Überblick über die Wirksamkeit und Anwendung der PID-Regelung zu geben. Dieses Papier wurde entwickelt, indem es eine kurze Einführung in Kontrollsysteme und verwandte Terminologien sowie die Motivation für das Projekt bietet. Es wurden Experimente und Beobachtungen gemacht, Vorzüge und Nachteile beschrieben bis hin zu den zukünftigen Verbesserungen. Ein Modell eines selbstausgleichenden Roboters wurde entwickelt, um die Wirksamkeit von PID in der Welt der Steuersysteme zu verstehen. Durch einige strenge Tests und Experimente wurden die Vor- und Nachteile des PID-Regelsystems entdeckt. Es hat sich herausgestellt, dass trotz vieler Vorteile der PID-Regelung gegenüber früheren Verfahren noch viele Verbesserungen an diesem System erforderlich sind. Wir hoffen, dass der Leser ein gutes Verständnis für die Bedeutung des Selbstausgleichs, die Wirksamkeit und die Mängel der PID-Regelung erhält

Schritt 1: Einführung

Mit dem Aufkommen von Computern und der Industrialisierung von Prozessen wurde in der gesamten Menschheitsgeschichte immer wieder daran geforscht, Prozesse zu verfeinern und vor allem maschinell autonom zu steuern. Der Zweck besteht darin, die Beteiligung des Menschen an diesen Prozessen zu reduzieren, wodurch die Fehler in diesen Prozessen reduziert werden. Daher wurde der Bereich „Control System Engineering“entwickelt. Control System Engineering kann definiert werden als die Verwendung verschiedener Methoden zur Steuerung des Ablaufs eines Prozesses oder zur Aufrechterhaltung einer konstanten und bevorzugten Umgebung, sei es manuell oder automatisch.

Ein einfaches Beispiel könnte die Temperaturregelung in einem Raum sein. Manuelle Steuerung bedeutet die Anwesenheit einer Person an einem Standort, die den aktuellen Zustand überprüft (Sensor), mit dem Sollwert vergleicht (Verarbeitung) und entsprechende Maßnahmen ergreift, um den Sollwert zu erhalten (Aktor). Das Problem bei dieser Methode besteht darin, dass sie nicht sehr zuverlässig ist, da eine Person bei ihrer Arbeit anfällig für Fehler oder Nachlässigkeit ist. Ein weiteres Problem besteht auch darin, dass die Geschwindigkeit des vom Aktuator eingeleiteten Prozesses nicht immer gleichförmig ist, was bedeutet, dass er manchmal schneller als erforderlich oder manchmal langsam ablaufen kann. Die Lösung dieses Problems bestand darin, einen Mikrocontroller zur Steuerung des Systems zu verwenden. Der Mikrocontroller ist

programmiert, um den Prozess gemäß gegebener Spezifikationen zu steuern, verbunden in einer Schaltung (wird später erörtert), speist den gewünschten Wert oder die gewünschten Bedingungen ein und steuert dadurch den Prozess, um den gewünschten Wert aufrechtzuerhalten. Der Vorteil dieses Verfahrens besteht darin, dass in diesem Verfahren kein menschliches Eingreifen erforderlich ist. Auch die Geschwindigkeit des Prozesses ist einheitlich

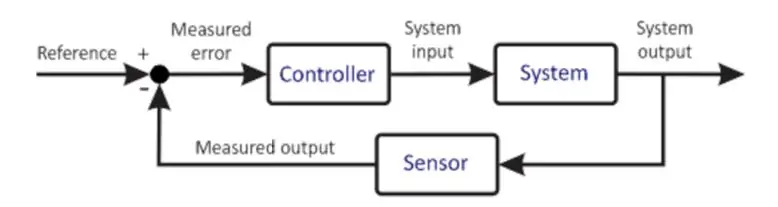
Grundsteuerungssystem

Das vorherige Diagramm zeigt eine sehr vereinfachte Version eines Kontrollsystems. Der Mikrocontroller ist das Herzstück eines jeden Kontrollsystems. Es ist eine sehr wichtige Komponente, daher sollte ihre Auswahl sorgfältig auf der Grundlage der Anforderungen des Systems erfolgen. Der Mikrocontroller empfängt eine Eingabe vom Benutzer. Dieser Eingang definiert den gewünschten Zustand des Systems. Der Mikrocontroller erhält auch eine Rückmeldung vom Sensor. Dieser Sensor ist mit dem Ausgang des Systems verbunden, dessen Informationen auf den Eingang zurückgeführt werden. Der Mikroprozessor führt aufgrund seiner Programmierung verschiedene Berechnungen durch und gibt eine Ausgabe an den Aktuator. Der Aktuator steuert die Anlage basierend auf dem Ausgang, um zu versuchen, diese Bedingungen beizubehalten. Ein Beispiel könnte ein Motortreiber sein, der einen Motor antreibt, wobei der Motortreiber der Aktor und der Motor die Anlage ist. Der Motor dreht sich somit mit einer bestimmten Geschwindigkeit. Der angeschlossene Sensor liest den aktuellen Zustand der Anlage und gibt diesen an den Mikrocontroller zurück. Der Mikrocontroller vergleicht erneut, führt Berechnungen durch und somit wiederholt sich der Zyklus. Dieser Prozess wiederholt sich und ist endlos, wobei der Mikrocontroller die gewünschten Bedingungen aufrechterhält

Schritt 2: PID-basiertes Regelsystem

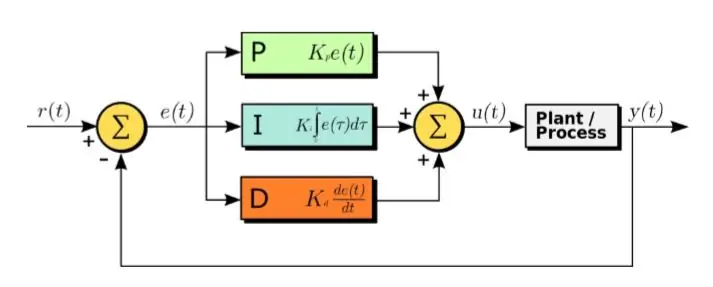
Der PID-Algorithmus ist eine effiziente Methode zum Entwerfen eines Steuersystems.

Definition

PID steht für Proportional, Integral und Derivative. Bei diesem Algorithmus ist das empfangene Fehlersignal die Eingabe. Und die folgende Gleichung wird auf das Fehlersignal angewendet

U(t) = Kp∗e(t) + Kd∗d/dt(e(t)) + Ki∗integral(e(t)) (1.1)

Kurze Erklärung

Wie in der obigen Gleichung zu sehen ist, werden das Integral und die Ableitung der Fehlersignale berechnet, mit ihren jeweiligen Konstanten multipliziert und zusammen mit der Konstanten Kp multipliziert mit e(t) addiert. Der Ausgang wird dann dem Aktuator zugeführt, der das System zum Laufen bringt. Schauen wir uns nun jeden Teil der Funktion der Reihe nach an. Diese Funktion wirkt sich direkt auf Anstiegszeit, Abfallzeit, Peak-Over-Shoot, Einschwingzeit und Dauerfehler aus.

• Proportionalteil: Der Proportionalteil reduziert die Anstiegszeit und verringert den stationären Fehler. Dies bedeutet, dass das System weniger Zeit braucht, um seinen Spitzenwert zu erreichen, und wenn es seinen stationären Zustand erreicht, wird der stationäre Fehler gering sein. Es erhöht jedoch das Spitzenüberschwingen.

• Differentialanteil: Der Differentialanteil reduziert das Überschwingen und die Einschwingzeit. Dies bedeutet, dass der Übergangszustand des Systems stärker gedämpft wird. Außerdem erreicht das System seinen stationären Zustand in kürzerer Zeit. Sie hat jedoch keinen Einfluss auf die Anstiegszeit oder den stationären Fehler.

• Integralanteil: Der Integralanteil reduziert die Anstiegszeit und eliminiert den stationären Fehler vollständig. Es erhöht jedoch das Spitzenüberschwingen und die Einschwingzeit.

• Abstimmung: Ein gutes Regelsystem hat eine geringe Anstiegszeit, Einschwingzeit, Spitzenüberschwinger und Dauerfehler. Daher müssen Kp, Kd, Ki fein abgestimmt werden, um den Beitrag der obigen Faktoren anzupassen, um ein gutes Kontrollsystem zu erhalten.

Die Abbildung ist beigefügt, die die Auswirkungen der Änderung verschiedener Parameter im PID-Algorithmus zeigt.

Schritt 3: Selbstausgleichender Roboter

Ein selbstausgleichender Roboter ist ein mehrschichtiger Zweiradroboter.

Der Roboter wird versuchen, sich bei der Anwendung von ungleichen Kräften auszugleichen. Es balanciert sich selbst durch die Anwendung einer Kraft aus, die der Resultierenden der Kräfte auf den Roboter entgegenwirkt.

Methoden des Selbstausgleichs

Es gibt vier Methoden des Selbstausgleichs von Robotern. Diese sind wie folgt:

Selbstausgleich mit zwei IR-Neigungssensoren

Dies ist eine der gröbsten Möglichkeiten, den Roboter auszubalancieren, da sie sehr wenig Hardware und einen relativ einfachen Algorithmus benötigt. Bei diesem Ansatz werden zwei gekippte IR-Sensoren verwendet, um den Abstand zwischen Boden und Roboter zu messen. Basierend auf der berechneten Distanz kann PID verwendet werden, um die Motoren anzutreiben, um den Roboter entsprechend auszubalancieren. Ein Nachteil dieser Methode ist, dass der IR-Sensor einige Messwerte verpassen kann. Ein weiteres Problem besteht darin, dass für die Berechnung der Entfernung ein Interrupt und Schleifen erforderlich sind, was die Zeitkomplexität des Algorithmus erhöht. Daher ist diese Methode zum Auswuchten des Roboters nicht sehr effizient.

Selbstausgleich mit Beschleunigungsmesser

Der Beschleunigungsmesser gibt uns die Beschleunigung des Körpers in 3 Achsen an. Beschleunigung orientiert in der y-Achse (aufwärts) und x-Achse (vorwärts) gibt uns das Maß, um die Richtung der Schwerkraft zu berechnen und damit den Neigungswinkel zu berechnen. Der Winkel wird wie folgt berechnet:

θ = arctan(Ay/Ax) (1.2)

Der Nachteil dieser Methode besteht darin, dass während der Bewegung des Roboters auch die horizontale Beschleunigung zu den Messwerten hinzugefügt wird, die ein hochfrequentes Rauschen ist. Daher ist der Neigungswinkel ungenau.

Selbstausgleich mit Gyroskop

Ein Gyroskop wird verwendet, um die Winkelgeschwindigkeiten entlang der drei Achsen zu berechnen. Der Neigungswinkel wird unter Verwendung der folgenden Gleichung erhalten.

θp(i) = θp(i−1) + 1/6(vali−3 + 2vali−2 + 2vali−1 + Vali) (1.3)

Ein großer Nachteil bei der Verwendung des Gyroskops ist, dass es eine kleine DC-Vorspannung hat, die ein niederfrequentes Rauschen ist und nach einiger Zeit die zurückgegebenen Werte völlig falsch sind. Dies führt nach der Integration dazu, dass der Nullpunkt wegdriftet. Dadurch bleibt der Roboter einige Zeit in seiner vertikalen Position und fällt um, sobald die Drift kommt.

Selbstausgleich mit Beschleunigungsmesser und Gyroskop

Wie oben besprochen, wird uns die Verwendung nur eines Beschleunigungsmessers oder eines Gyroskops nicht den richtigen Neigungswinkel liefern. Um dies zu berücksichtigen, werden sowohl Beschleunigungsmesser als auch Gyroskop verwendet. Diese sind beide in MPU6050 eingebettet. In diesem erhalten wir die Daten von beiden und fusionieren sie dann entweder mit dem Kalman-Filter oder dem Komplementärfilter.

• Kalman-Filter: Der Kalman-Filter berechnet die beste Schätzung des Zustands eines dynamischen Systems aus verrauschten Messungen und minimiert den mittleren quadratischen Fehler der Schätzung. Es arbeitet in zwei Stufen, Vorhersage und Korrektur, angesichts der diskreten stochastischen Gleichungen, die die Systemdynamik beschreiben. Es ist jedoch ein sehr komplexer Algorithmus, insbesondere auf einer begrenzten Hardware eines Mikrocontrollers zu implementieren.

• Komplementärfilter: Dieser Algorithmus verwendet hauptsächlich die vom Gyroskop erhaltenen Daten und integriert sie im Laufe der Zeit, um den Neigungswinkel zu erhalten. Es verwendet auch einen kleinen Teil der Beschleunigungsmesser-Messwerte. Der komplementäre Filter minimiert tatsächlich das hochfrequente Rauschen des Beschleunigungsmessers und das niederfrequente Rauschen des Gyroskops und verschmilzt sie dann, um den besten genauen Neigungswinkel zu erhalten.

Schritt 4: Design des Roboters

Wir haben einen selbstausgleichenden Roboter mit Proportional Derivative Controller entwickelt, der von Complementary Filter für MPU6050 implementiert wird. Dieses kleine Modell eines selbstausgleichenden Roboters wird uns die Nützlichkeit von Steuerungssystemen beim Selbstausgleich von Robotern veranschaulichen.

Systemimplementierung:

Das System ist ein selbstausgleichender Roboter. Es wird unter Verwendung des PID-Controllers implementiert, der ein Proportional-Integral-Derivative-Controller ist. Wir balancieren den Roboter, indem wir seine Räder in Fallrichtung antreiben. Dabei versuchen wir, den Schwerpunkt des Roboters über dem Drehpunkt zu halten. Um die Räder in Fallrichtung anzutreiben, sollten wir wissen, wo der Roboter fällt und mit welcher Geschwindigkeit er fällt. Diese Daten werden mit MPU6050 erhalten, das über einen Beschleunigungsmesser und ein Gyroskop verfügt. MPU6050 misst den Neigungswinkel und gibt seine Ausgabe an den Micro-Controller. MPU6050 ist über I2C mit dem STM-Board verbunden. In I2C ist ein Draht für die Uhr, die als SCL bezeichnet wird. Die andere ist für die Datenübertragung, die SDA ist. Dabei wird die Master-Slave-Kommunikation verwendet. Startadresse und Endadresse werden angegeben, um zu wissen, wo die Daten beginnen und wo sie enden. Wir haben hier den Complementary Filter für MPU6050 implementiert, einen mathematischen Filter zum Zusammenführen der Ausgänge von Beschleunigungsmesser und Gyroskop. Nach dem Abrufen der Daten von MPU6050 führt der Mikrocontroller Berechnungen durch, um zu wissen, wo er fällt. Basierend auf den Berechnungen gibt der STM-Mikrocontroller dem Motorfahrer Befehle, um die Fahrzeuge in Fallrichtung zu fahren, wodurch der Roboter ausgeglichen wird.

Schritt 5: Projektkomponenten

Folgende Komponenten wurden im Projekt des selbstbalancierenden Roboters verwendet:

STM32F407

Ein von ST Microelectronics entwickelter Mikrocontroller. Es funktioniert auf der ARM-Cortex-M-Architektur.

Motortreiber L298N

Dieser IC wird verwendet, um den Motor zu betreiben. Es bekommt zwei externe Eingänge. Einer vom Mikrocontroller, der ihm ein PWM-Signal liefert. Durch Einstellen der Impulsbreite kann die Motordrehzahl angepasst werden. Sein zweiter Eingang ist die Spannungsquelle, die zum Antrieb des Motors benötigt wird, in unserem Fall eine 12-V-Batterie.

Gleichstrommotor

Ein Gleichstrommotor wird mit Gleichstrom betrieben. In diesem Experiment läuft der DC-Motor mit den Optokopplern, die an den Motortreiber angeschlossen sind. Zum Antrieb des Motors haben wir den Motor Drive L298N verwendet.

MPU6050

MPU6050 wird verwendet, um Informationen darüber zu erhalten, wo der Roboter fällt. Es misst den Neigungswinkel in Bezug auf den Neigungsnullpunkt, der die Position des MPU6050 beim Start des Programms ist.

Der MPU6050 verfügt über einen 3-Achsen-Beschleunigungsmesser und ein 3-Achsen-Gyroskop. Der Beschleunigungsmesser misst die Beschleunigung entlang der drei Achsen und das Gyroskop misst die Winkelgeschwindigkeit um die drei Achsen. Um die Ausgabe zu kombinieren, müssen wir die Geräusche beider herausfiltern. Um die Geräusche herauszufiltern, haben wir Kalman- und Komplementärfilter. Wir haben Komplementärfilter in unserem Projekt implementiert.

Optopaar 4N35

Ein Optokoppler ist ein Gerät, das verwendet wird, um den Niederspannungsteil und den Hochspannungsteil der Schaltung zu isolieren. Wie der Name schon sagt, funktioniert es auf der Basis von Licht. Wenn der Niederspannungsteil ein Signal erhält, fließt Strom im Hochspannungsteil

Schritt 6: Struktur des Roboters

Der Aufbau des Roboters wird wie folgt erklärt:

Physikalische Struktur

Der selbstbalancierende Roboter besteht aus zwei Schichten aus transparentem Kunststoffglas. Die Details von zwei Schichten sind unten angegeben:

Erste Schicht

Im unteren Teil der ersten Schicht haben wir eine Zelle zur Stromversorgung des STM-Boards platziert. Außerdem wurden auf jeder Seite zwei Motoren mit je 4 Volt angebracht, an denen Reifen angeschlossen sind, damit sich der Roboter bewegen kann. Im oberen Teil der ersten Schicht wurden zwei Batterien mit je 4 Volt (insgesamt 8 Volt) und ein Motortreiber-IC (L298N) für den Betrieb von Motoren platziert.

Zweite Schicht

In der oberen Schicht des Roboters haben wir das STM Board auf Perf Board platziert. Auf der obersten Lage wird ein weiteres Perfboard mit 4 Optokopplern platziert. Das Gyroskop wird auch von der Unterseite auf die oberste Schicht des Roboters gelegt. Beide Komponenten sind im Mittelteil platziert, damit der Schwerpunkt möglichst niedrig gehalten wird.

Schwerpunkt des Roboters

Der Schwerpunkt wird so niedrig wie möglich gehalten. Dazu haben wir auf der unteren Lage schwere Batterien und auf der oberen Lage leichte Bauteile wie STM-Board und Optokoppler platziert.

Schritt 7: Code

Code wurde auf Atollic TrueStudio kompiliert. STM Studio wurde für Debugging-Zwecke verwendet.

Schritt 8: Fazit

Nach viel Experimentieren und Beobachten kommen wir schließlich zu dem Punkt, an dem wir unsere Ergebnisse zusammenfassen und diskutieren, inwieweit es uns gelungen ist, die Wirksamkeit des Systems zu implementieren und herauszuarbeiten.

Allgemeine Bewertung

Während des Experimentierens wurde die Drehzahl des Motors erfolgreich mit dem PID-Algorithmus gesteuert. Die Kurve ist jedoch nicht gerade eine glatte gerade Linie. Dafür gibt es viele Gründe:

• Obwohl der Sensor an einen Tiefpassfilter angeschlossen ist, bietet er immer noch gewisse endliche Entprellungen; diese sind auf die nichtlinearen Widerstände und einige unvermeidliche Gründe der analogen Elektronik zurückzuführen.

• Der Motor dreht sich bei kleiner Spannung oder PWM nicht gleichmäßig. Es erzeugt Ruckeln, die zu falschen Werten führen können, die dem System zugeführt werden.

• Aufgrund von Wackeln kann der Sensor einige Schlitze verpassen, die höhere Werte liefern. • Ein weiterer Hauptgrund für Fehler kann die Kerntaktfrequenz des STM-Mikrocontrollers sein. Dieses Modell des STM-Mikrocontrollers bietet einen Kerntakt von 168 MHz. Obwohl dieses Problem in diesem Projekt behandelt wurde, gibt es eine allgemeine Vorstellung von diesem Modell, dass es nicht genau eine so hohe Frequenz liefert.

Die Open-Loop-Geschwindigkeit liefert eine sehr glatte Linie mit nur wenigen unerwarteten Werten. Der PID-Algorithmus funktioniert auch gut und bietet eine sehr geringe Einschwingzeit des Motors. Der PID-Algorithmus des Motors wurde unter verschiedenen Spannungen getestet, um die Referenzdrehzahl konstant zu halten. Die Spannungsänderung ändert die Drehzahl des Motors nicht und zeigt an, dass der PID-Algorithmus einwandfrei funktioniert

Wirksamkeit

Hier diskutieren wir die Wirksamkeit des PID-Reglers, die wir während des Experimentierens beobachtet haben.

Einfache Implementierung

Wir haben im Abschnitt Experimente und Beobachtungen gesehen, dass ein PID-Regler sehr einfach zu implementieren ist. Es erfordert nur drei Parameter oder Konstanten, die eingestellt werden müssen, um ein Geschwindigkeitsregelsystem zu haben

Unübertroffene Effizienz für lineare Systeme

Der lineare PID-Regler ist der effizienteste in der Familie der Regler, da die Logik sehr einfach ist und die Anwendung bei linearen oder ziemlich linearen Anwendungen weit verbreitet ist.

Einschränkungen

Wir haben in der Zusammenfassung die Grenzen dieses Systems erklärt. Hier besprechen wir einige von ihnen, die wir beobachtet haben.

Auswahl von Konstanten

Wir haben gesehen, dass, obwohl ein PID-Regler leicht zu implementieren ist, es dennoch ein Hauptnachteil des Systems ist, dass der Schritt der Auswahl des Wertes von Konstanten mühsam ist; da man schwierige Berechnungen anstellen muss. Der andere Weg ist die Hit-and-Trial-Methode, aber auch das ist nicht effizient.

Konstanten nicht immer konstant

Die experimentellen Ergebnisse zeigten, dass bei unterschiedlichen Werten der Referenzdrehzahl für den Motor der PID-Regler bei den gleichen Werten der PID-Konstanten eine Fehlfunktion hatte. Für unterschiedliche Geschwindigkeiten mussten die Konstanten unterschiedlich gewählt werden, was den Rechenaufwand exponentiell erhöht.

Nicht linear

Der in unserem Fall verwendete PID-Regler ist linear und kann daher nur auf lineare Systeme angewendet werden. Bei nichtlinearen Systemen muss der Regler anders implementiert werden. Obwohl verschiedene nichtlineare PID-Methoden verfügbar sind, erfordern sie die Auswahl weiterer Parameter. Dies macht das System wiederum aufgrund hoher Rechenkosten unerwünscht.

Erster Push erforderlich

Wir haben im Experimentierabschnitt gezeigt, dass bei einer relativ kleinen Referenzdrehzahl, bei der der Fehler beim Start ziemlich klein ist, die vom PID gelieferte PWM so klein ist, dass sie nicht das erforderliche Startdrehmoment für den Motor erzeugt. So läuft der Motor in einigen Versuchen nicht oder liefert in anderen Versuchen ein großes Überschwingen und eine längere Einschwingzeit.

Schritt 9: Besonderer Dank

Besonderer Dank gilt meinen Gruppenmitgliedern, die mir bei diesem Projekt geholfen haben.

Den Link zum Video lade ich demnächst hoch.

Ich hoffe, Sie finden dieses instructable interessant.

Das ist Tahir Ul Haq von UET, der sich abmeldet. Danke schön !!!