So erstellen Sie eine geodätische Kuppel im Temcor-Stil in Autodesk Inventor - Gunook

2025 Autor: John Day | [email protected]. Zuletzt bearbeitet: 2025-01-23 12:52

Dieses Tutorial zeigt Ihnen, wie Sie mit ein wenig Mathematik eine Kuppel im Temcor-Stil erstellen.

Die meisten Informationen in diesem Tutorial stammen aus TaffGochs Reverse-Engineering der Unterteilungsmethode der alten Amundsen-Scott-Südpolstation, also ein großes Dankeschön an ihn!

Ein großer Vorteil von Temcor-Kuppeln ist ihre geringe Anzahl einzigartiger Streben - sie nimmt rechnerisch mit der Frequenz zu, ähnlich wie Duncan Stuarts regelmäßiges triacontaedrisches geodätisches Gitter (Methode 3*), aber das Ergebnis sieht viel erfreulicher aus.

Der Einfachheit halber beträgt die Frequenz der Kuppel, die wir herstellen, 14, sodass die Akkordfaktoren mit dem Temcor-Modell von TaffGoch verglichen werden können.

Die.ipt-Datei von Inventor 2016 ist am Ende des Tutorials enthalten.

*AKTUALISIEREN*

Ich habe Methode 4 als regelmäßiges triacontaedrisches geodätisches Gitter von Duncan Stuart beschrieben, aber das ist es nicht. Die Methode wurde tatsächlich von Christopher Kitrick erfunden, der in seinem 1985 erschienenen Artikel "Geodesic Domes" seine Konstruktion beschrieb. Darüber hinaus skizziert er in seinem 1990 erschienenen Artikel "A Unified Approach to Class I, II & III Geodesic Domes" 8 weitere Methoden, eine davon ist Duncan Stuarts Methode 3, die andere seine eigene "Methode 4", und überraschenderweise genug, eine Methode analog zu der von Temcor, die er "Methode aa" nennt (Schritt 7 zeigt, wie Temcor "Methode aa" modifiziert). In einem zukünftigen instructable werde ich die Konstruktion der Methoden beschreiben, die im letzteren Papier beschrieben werden.

Schritt 1: Benutzerparameter

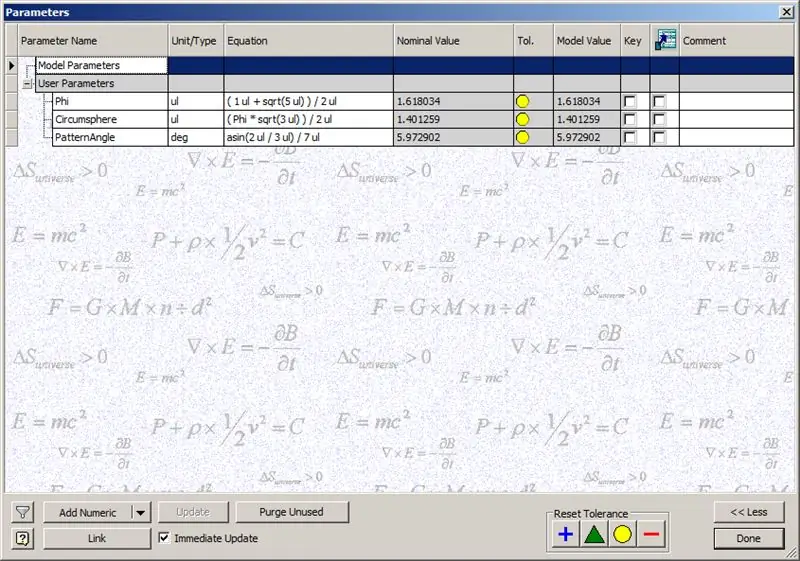
Bevor wir mit dem Bau der Kuppel beginnen, geben Sie die angezeigten Parameter ein:

Phi - Der Goldene Schnitt. Definiert als ((1+√5/)2

Zirkumsphäre - Dies ist die Zirkumsphäre eines Dodekaeders, definiert als ((Phi*√3)/2)

PatternAngle - Dies ist der zentrale Winkel eines Dodekaeders. Da die Frequenz unserer Kuppel 14 beträgt, teilen wir diesen Zentralwinkel durch die Hälfte der Frequenz, in diesem Fall 7.

Schritt 2: Skizzieren eines goldenen Rechtecks

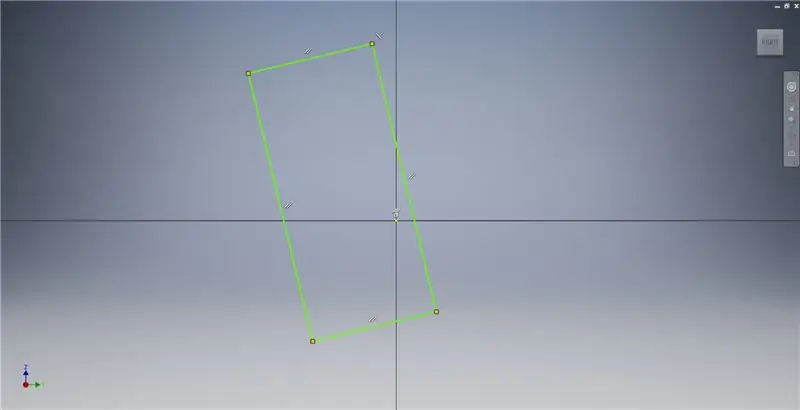
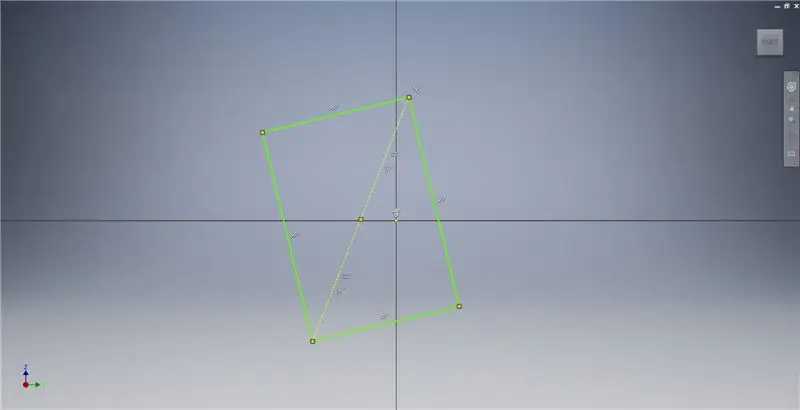
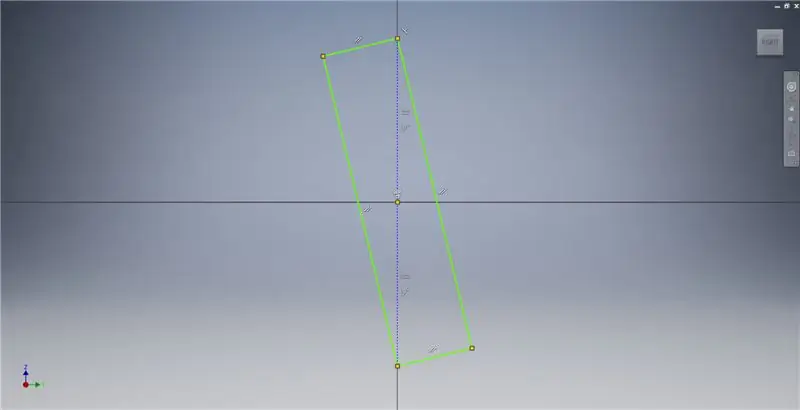
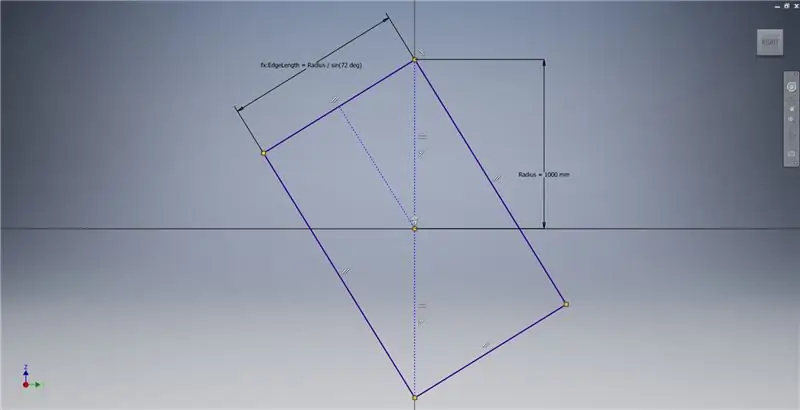
Beginnen Sie mit einer Skizze auf der YZ-Ebene und erstellen Sie dann wie gezeigt ein Drei-Punkte-Rechteck. Weitere Informationen zur Erstellung eines Goldenen Rechtecks finden Sie in den Bildnotizen.

Schritt 3: Erstellen eines Golden² Rechtecks

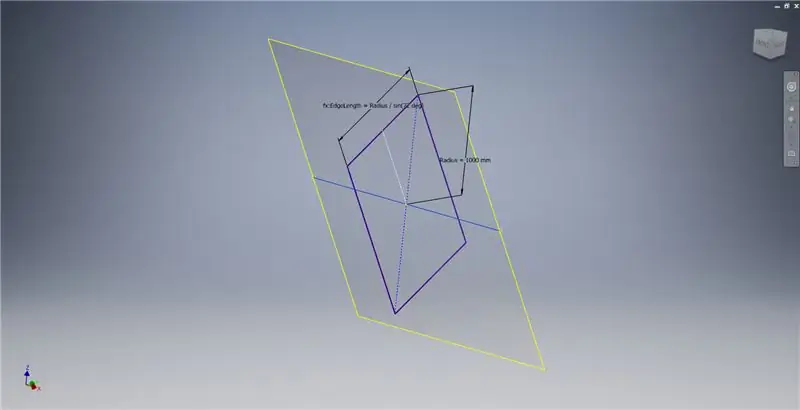
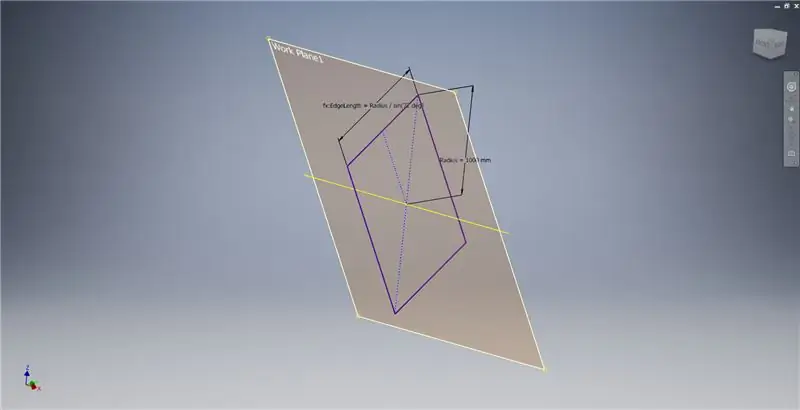
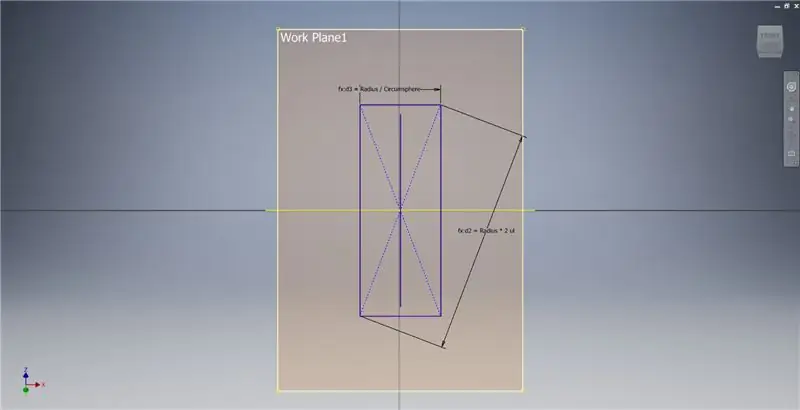
Erstellen Sie eine Arbeitsebene mit der X-Achse und der im ersten Bild markierten Linie und beginnen Sie dann eine weitere Skizze auf dieser Arbeitsebene. Konstruieren Sie ein Mittelpunktrechteck ausgehend vom Ursprung und bemaßen Sie das Rechteck dann wie im dritten Bild gezeigt.

Schritt 4: Erstellen des 2v-Triacon-Dreiecks

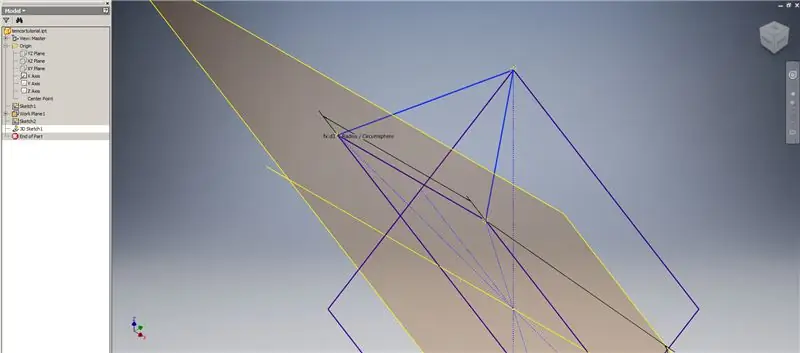
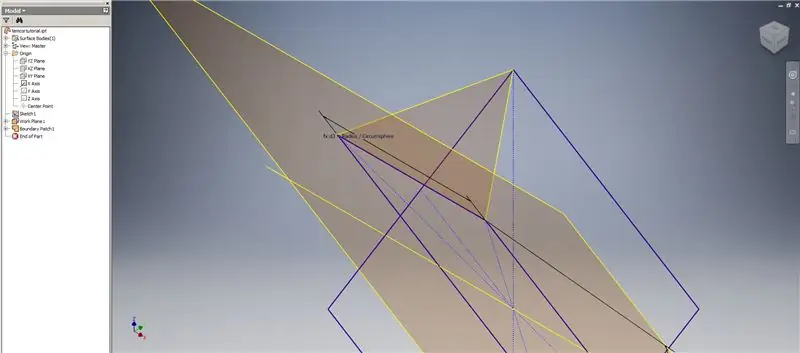
Jetzt, da wir die gesamte Geometrie haben, die wir benötigen, bilden Sie das Grenzfeld im zweiten Bild mit der von Ihnen bevorzugten Methode. Ich habe mich für eine 3D-Skizze entschieden, aber das Skizzieren auf einer anderen Arbeitsebene würde genauso gut funktionieren.

Schritt 5: Erstellen der Schnittebenen

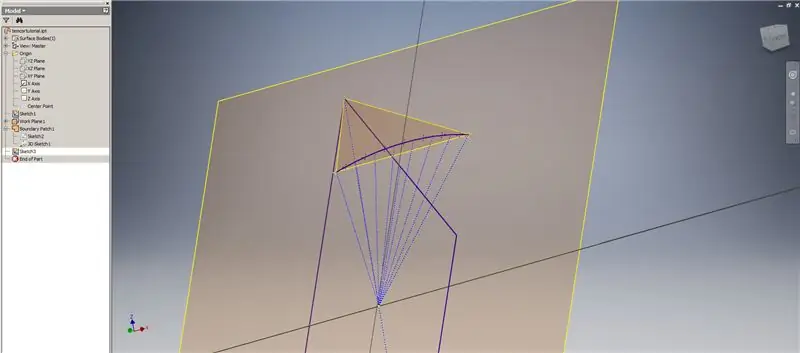
Beginnen Sie eine weitere Skizze auf der ersten von Ihnen erstellten Arbeitsebene ("Arbeitsebene 1"), projizieren Sie die Ecken des Golden²-Rechtecks und verbinden Sie dann diese Punkte und den Ursprung, um den Zentralwinkel des 2v-Trikontaeders zu bilden. Teilen Sie es durch die Hälfte der Frequenz der Kuppel, als ob Sie eine Aufschlüsselung nach Methode 2 beginnen würden. Platziere Punkte auf den Mittelpunkten der Akkorde.

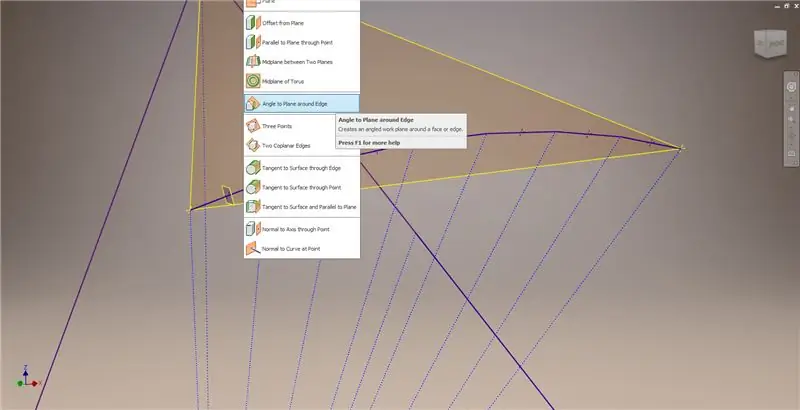
Verlassen Sie die Skizze und erstellen Sie eine Ebene mit einem der Akkorde und seinem Mittelpunkt, wie im zweiten Bild gezeigt. Erstellen Sie dann eine weitere Arbeitsebene mit "Winkel zu Ebene um Kante". Wählen Sie Arbeitsebene 1 und eine der Konstruktionslinien aus, die im mittleren rechten und unteren linken Bild angezeigt werden. Akzeptieren Sie den Standardwinkel von 90 Grad, sonst würde der Rest der Unterteilung nicht richtig aussehen. Wiederholen Sie den Vorgang mit den restlichen Akkorden und Konstruktionslinien, um das Ergebnis im unteren rechten Bild zu erhalten.

Schritt 6: Erstellen der Schnittkurven und Bilden der Unterteilung

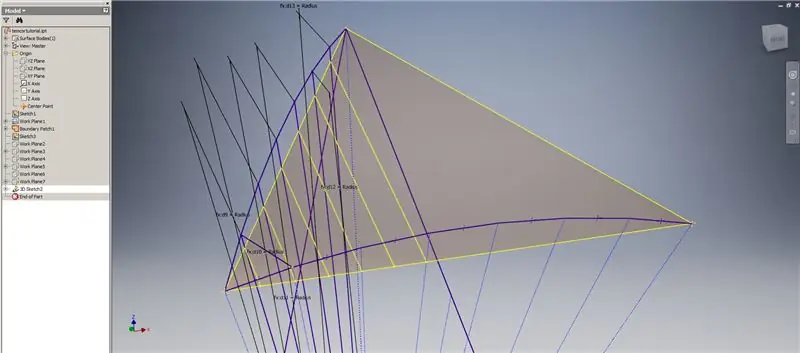
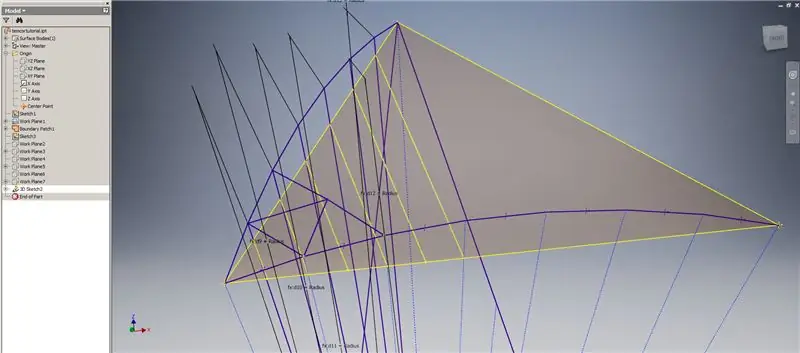
Beginnen Sie mit einer 3D-Skizze und erstellen Sie dann Schnittkurven mit den gerade erstellten Arbeitsebenen und dem Begrenzungspatch, um die im oberen Bild gezeigten Linien zu bilden.

Zeichnen Sie Linien, die mit den Endpunkten der Schnittkurven zusammenfallen, wie in Abbildung 2 gezeigt. Machen Sie sie alle gleich dem Radius der Kuppel. Zeichnen Sie die Sehnen, die die Linien verbinden, die auf den Schnittkurven liegen. Verbinden Sie jede Geometrie, die nahe genug aussieht, um ein Dreieck der Unterteilung zu bilden. Sehen Sie sich die nächsten 10 Bilder an, welche Akkorde über die Schnittebenen gespiegelt werden sollen – sie können es besser erklären als bloße Worte.

Schritt 7: Fertigstellung der Kuppel

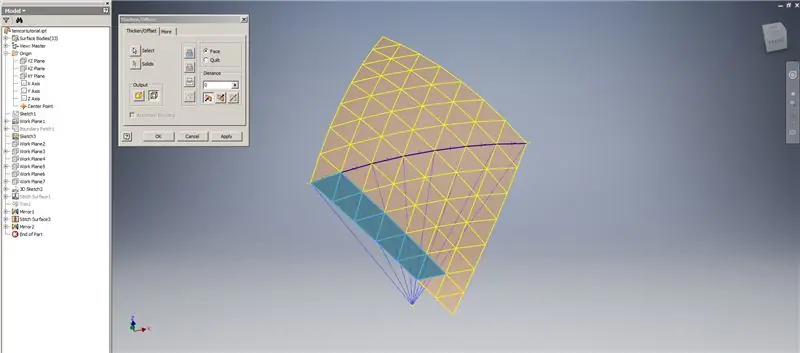
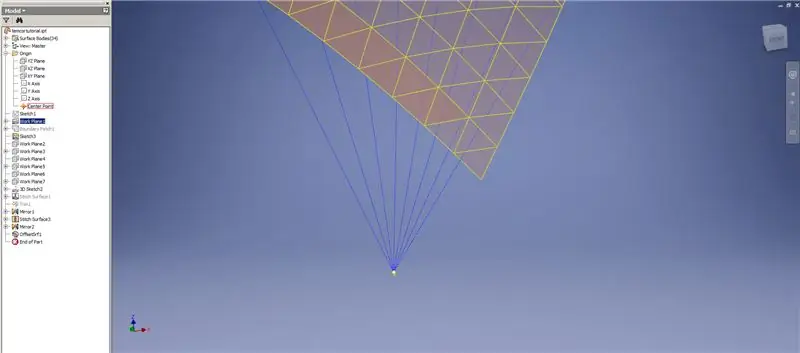
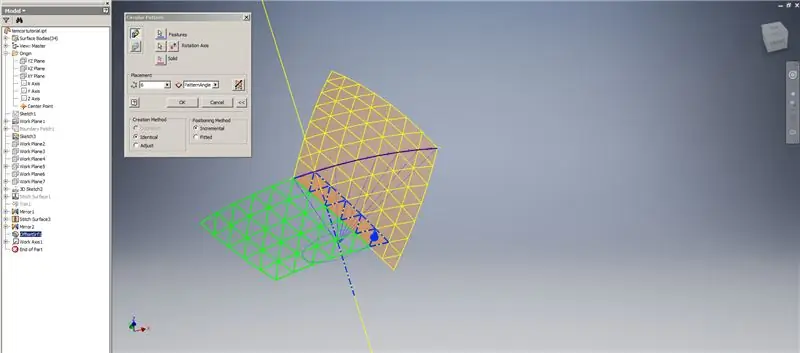
Erstellen Sie eine Verdickung/Versatz der unteren Reihen und lassen Sie die letzten beiden Reihen von Dreiecken aus. Mustern Sie das neue OffsetSrf 6 Mal oder ((Frequenz=14)/2)-1. Blenden Sie OffsetSrf aus, sticken Sie die gemusterten Flächen und spiegeln Sie dann die gestickte Fläche mit der YZ-Ebene. Erstellen Sie Arbeitsebenen, die auf den Scheitelpunkten des oberen Dreiecks ruhen, wie in Abbildung 6 gezeigt. Trimmen Sie die genähten und gespiegelten Flächen mit diesen neuen Arbeitsebenen und nähen Sie dann die verbleibenden Flächen zusammen. Mustern Sie diese letzte Fläche entlang der Z-Achse, nähen Sie dann diese letzten Flächen zusammen, und Sie sind fertig!

Schritt 8: Akkorde überprüfen

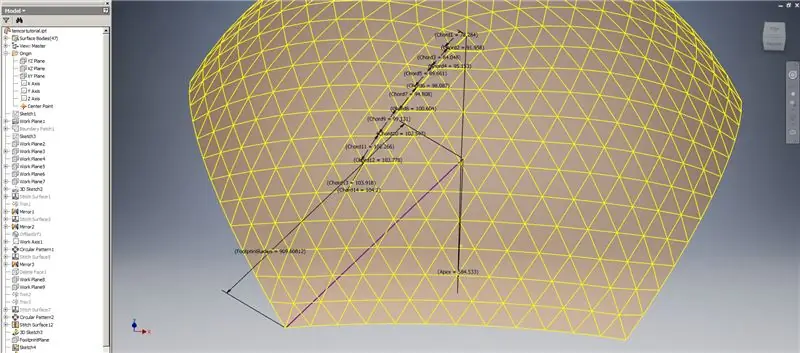
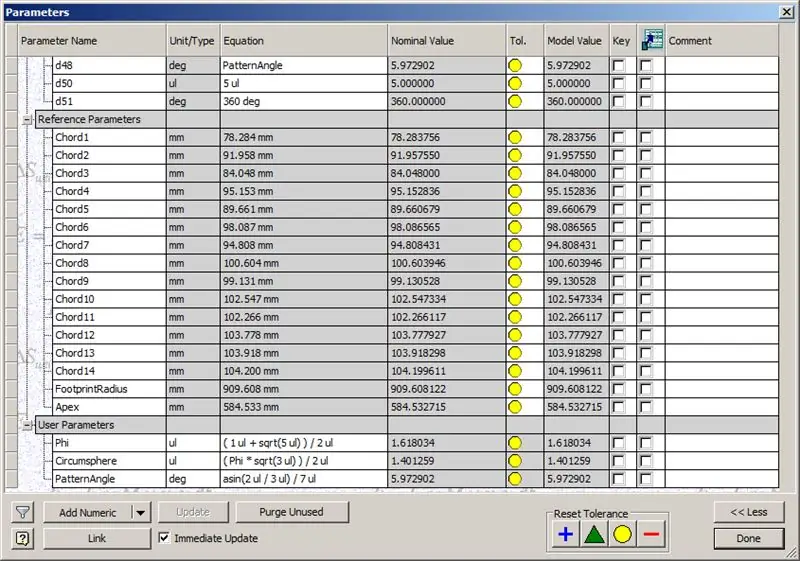
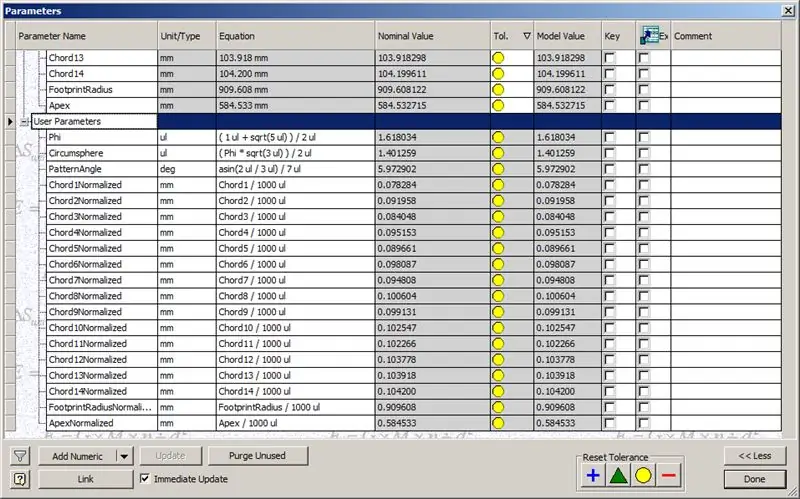
Unsere Kuppel ist also fertig, aber mal sehen, ob die Zahlen mit dem Modell von TaffGoch übereinstimmen:

Wenn man sich die Referenzparameter ansieht, sieht es so aus, als ob sie perfekt zusammenpassen!

Wenn wir die Sehnenlängen durch 1000 teilen, können wir deutlich eine perfekte Übereinstimmung mit den Sehnenfaktoren des TaffGoch-Modells sowie dem Footprint-Radius und den Apex-Faktoren sehen.