
Inhaltsverzeichnis:
- Schritt 1: Lesen Sie das folgende Problem
- Schritt 2: Identifizieren
- Schritt 3: Verwenden Sie die folgende Formel, um den "z-Score" zu finden
- Schritt 4: Subtrahieren Sie den Ablehnungsgrad von "1"
- Schritt 5: Zweiseitiger oder einseitiger Test?
- Schritt 6: Zusätzlicher Schritt für den zweiseitigen Test
- Schritt 7: Verwenden Sie die Z-Tabelle
- Schritt 8: Ablehnung der Nullhypothese oder Ablehnung der Nullhypothese
- Schritt 9: Bestimmen der statistischen Signifikanz
- Schritt 10: Überprüfen Sie Ihre Antworten
- Autor John Day day@howwhatproduce.com.
- Public 2024-01-30 07:18.
- Zuletzt bearbeitet 2025-06-01 06:08.

Überblick:
Zweck: In diesem anweisbaren erfahren Sie, wie Sie feststellen können, ob zwischen zwei Variablen in Bezug auf ein Problem der Sozialarbeit eine statistische Signifikanz besteht. Sie werden einen Z-Test verwenden, um diese Signifikanz zu bestimmen.
Dauer: 10-15 Minuten, 10 Schritte
Zubehör: Schreibgerät, Papier und Taschenrechner
Schwierigkeitsgrad: Benötigt Grundkenntnisse der Algebra
Begriffe (in alphabetischer Reihenfolge):
Berechneter Mittelwert - Der Durchschnitt der vom Tester ermittelten Werte
Populationsgröße - In der Statistik alle Personen, Objekte oder Ereignisse, die die Untersuchungskriterien erfüllen
Nullhypothese - Die Aussage, dass es keine Beziehung zwischen zwei interessierenden Variablen gibt
Ablehnungsniveau - Ausgewähltes Wahrscheinlichkeitsniveau, bei dem die Nullhypothese abgelehnt wird
Zweiseitig - Die Beziehung zwischen den Variablen geht in beide Richtungen, was bedeutet, dass der Test bestimmt, ob eine Variable einen Gesamteffekt auf die andere Variable hat. Ex. Unter den medizinischen Sozialarbeitern unterscheiden sich Frauen und Männer in ihrer Arbeitszufriedenheit
Einseitig - die Beziehung zwischen den Variablen weist in eine bestimmte Richtung. Ex. Weibliche medizinische Sozialarbeiter haben eine höhere Arbeitszufriedenheit als männliche medizinische Sozialarbeiter
Statistische Signifikanz - Aufgrund eines Stichprobenfehlers als zu unwahrscheinlich beurteilt, dass es aufgetreten ist
Wahrer/erwarteter Mittelwert - Der ursprüngliche Durchschnitt der Werte
Wahre Standardabweichung - Wie stark ein Satz von Werten variiert; ermöglicht es uns herauszufinden, wie wahrscheinlich es ist, dass ein bestimmter Wert durch einen Z-Test erhalten wird
Z-Score - Ein Maß dafür, wie viele Standardabweichungen unter oder über der Grundgesamtheit einen Score bedeuten
Z-Test - Ein Hypothesentestverfahren, das verwendet wird, um zu entscheiden, ob Variablen statistische Signifikanz haben
Z-Tabelle - Eine Tabelle zur Berechnung der statistischen Signifikanz
Schritt 1: Lesen Sie das folgende Problem
Ich interessiere mich für die Untersuchung von Angstzuständen bei Studenten, die für Midterms studieren. Ich weiß, dass der wahre Mittelwert auf der Angstskala aller Studenten 4 ist, mit einer echten Standardabweichung von 1. Ich studiere eine Gruppe von 100 Studenten, die für die Zwischensemester studieren. Ich berechne einen Mittelwert für diese Schüler auf dieser Skala von 4,2. (Hinweis: höhere Werte = höhere Angst). Der Ablehnungsgrad beträgt 0,05. Gibt es auf dieser Skala einen statistisch signifikanten Unterschied zwischen der allgemeinen Studierendenpopulation und den Studierenden, die für ein Midterm-Studium studieren?
Schritt 2: Identifizieren
A. Der wahre Mittelwert (erwarteter Mittelwert)
B. Die wahre Standardabweichung der Grundgesamtheit
C. Der berechnete Mittelwert (beobachteter Mittelwert)
D. Die Bevölkerungszahl
e. Die Ablehnungsstufe
Schritt 3: Verwenden Sie die folgende Formel, um den "z-Score" zu finden

z = (beobachteter Mittelwert - erwarteter Mittelwert)
(Standardabweichung/√Populationsgröße)
Schritt 4: Subtrahieren Sie den Ablehnungsgrad von "1"
Notieren Sie diesen Wert
Schritt 5: Zweiseitiger oder einseitiger Test?
Definitionen und Beispiele für zweiseitige und einseitige Tests finden Sie am Anfang des anweisbaren Abschnitts mit dem Titel: "Begriffe"
Schreiben Sie auf, ob der Test zweiseitig oder einseitig ist.
Schritt 6: Zusätzlicher Schritt für den zweiseitigen Test
Wenn der Test einseitig ist, lassen Sie die in Schritt 3 berechnete Zahl unverändert. Wenn es zweiseitig ist, teilen Sie den Wert, den Sie aus Schritt 3 berechnet haben, in zwei Hälften.
Schreiben Sie diese Nummer auf.
Schritt 7: Verwenden Sie die Z-Tabelle


Greifen Sie auf die Z-Tabelle zu, die die erste Tabelle in diesem Schritt ist. Verwenden Sie die Nummer, die Sie in Schritt 6 notiert haben, und suchen Sie sie in der Mitte der Tabelle. Wenn Sie die Zahl in der Mitte gefunden haben, verwenden Sie die Spalte ganz links und die obere Reihe, um den Wert zu bestimmen.
Schreiben Sie den Wert. Für weitere Anweisungen zum Ermitteln dieses Werts finden Sie im Folgenden ein Beispiel für die Verwendung der Z-Tabelle:
Wenn Ihre in Schritt 6 berechnete Zahl „0,0438“wäre, wie im Querschnitt von Spalte 3 und Zeile 3 im Auszug der Z-Tabelle zu finden, wäre Ihr Wert 0,11. Die Spalte ganz links der Tabelle hat den Wert der ersten Dezimalstelle. Die oberste Zeile enthält den Wert für die zweite Dezimalstelle. Siehe das zweite Bild eines Auszugs der z-Tabelle für ein Beispiel.
Schritt 8: Ablehnung der Nullhypothese oder Ablehnung der Nullhypothese
Vergleichen Sie die Zahl, die Sie in Schritt 7 gefunden haben, mit der Zahl, die Sie in Frage 3 berechnet haben, um festzustellen, ob Sie die Nullhypothese ablehnen oder ob Sie die Nullhypothese nicht ablehnen sollen.
Notieren Sie die Nummer aus Schritt 3 Notieren Sie die Nummer aus Schritt 7
Wenn die Zahl, die Sie in Schritt 7 berechnet haben, kleiner ist als die Zahl, die Sie in Schritt 3 berechnet haben, müssen Sie die Nullhypothese verwerfen. Wenn die Zahl, die Sie in Schritt 7 berechnet haben, größer ist als die Zahl, die Sie in Schritt 3 berechnet haben, verwerfen Sie die Nullhypothese nicht
Die Nullhypothese ablehnen oder die Nullhypothese nicht ablehnen?
Schritt 9: Bestimmen der statistischen Signifikanz
Wenn Sie die Nullhypothese ablehnen, besteht eine statistische Signifikanz zwischen den Variablen. Wenn Sie die Nullhypothese nicht ablehnen, besteht keine statistische Signifikanz zwischen den Variablen.
Schreiben Sie auf, ob es eine statistische Signifikanz gibt oder nicht
Schritt 10: Überprüfen Sie Ihre Antworten
- Schritt 3: 2
- Schritt 5: Zweischwänzig
- Schritt 6: 0,475
- Schritt 7: 1,96
- Schritt 8: Da 1,96 < 2, müssen Sie die Nullhypothese verwerfen
- Schritt 9: Es gibt eine statistische Signifikanz
Empfohlen:
Heimwerken -- Einen Spinnenroboter herstellen, der mit einem Smartphone mit Arduino Uno gesteuert werden kann – wikiHow

Heimwerken || Wie man einen Spider-Roboter herstellt, der mit einem Smartphone mit Arduino Uno gesteuert werden kann: Während man einen Spider-Roboter baut, kann man so viele Dinge über Robotik lernen. Wie die Herstellung von Robotern ist sowohl unterhaltsam als auch herausfordernd. In diesem Video zeigen wir Ihnen, wie Sie einen Spider-Roboter bauen, den wir mit unserem Smartphone (Androi
So erstellen Sie einen Smart Pot mit NodeMCU, der von der App gesteuert wird – wikiHow

So erstellen Sie einen Smart Pot mit NodeMCU, der von einer App gesteuert wird: In dieser Anleitung bauen wir einen Smart Pot, der von einem ESP32 und einer Anwendung für Smartphones (iOS und Android) gesteuert wird. Wir verwenden NodeMCU (ESP32) für die Konnektivität und die Blynk-Bibliothek für das Cloud-IoT und die Anwendung auf dem Smartphone. Endlich haben wir
So schalten Sie jedes Gerät aus der Ferne ein, z. einen Computer (mit einem Mobiltelefon): 5 Schritte
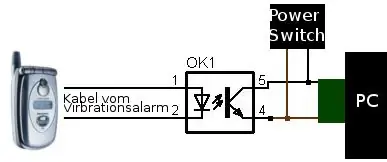
So schalten Sie jedes Gerät aus der Ferne ein, z. ein Computer (mit einem Mobiltelefon): In diesem anweisbaren zeige ich Ihnen, wie Sie ein altes Mobiltelefon in einen Fernschalter für Ihren Computer verwandeln. Für andere Geräte siehe letzter Schritt. Dies ist fast kostenlos, wenn Sie ein altes Handy und eine SIM-Karte besitzen. Was Sie brauchen: - Altes Handy (w
So reparieren Sie einen Wechselrichter mit LCD-Hintergrundbeleuchtung. Mit einem Fujiplus FP-988D. für 0 $.: 9 Schritte

So reparieren Sie einen Wechselrichter mit LCD-Hintergrundbeleuchtung. Mit einem Fujiplus FP-988D. für $ 0.: In diesem anweisbaren werde ich Sie durch die Reparatur eines toten LCD-Hintergrundlicht-Wechselrichters mit den Teilen führen, die Sie haben. Sie können feststellen, ob Sie ein totes Gegenlicht haben, indem Sie zuerst andere Möglichkeiten ausschließen. Monitor auf mehreren Computern überprüfen. Stellen Sie sicher, dass
So kommunizieren Sie mit einem Alien-Artefakt oder . . .: 4 Schritte (mit Bildern)
Wie man mit einem außerirdischen Artefakt kommuniziert oder…: *** Enge Begegnungen der seltsam-minzigen Art. *** Dieses Instructable zeigt Ihnen, wie Sie eine Altoids-Version des Mutterschiffs "Close Encounters" bauen und damit interagieren. Dies kann ein wichtiges Training für den Tag sein, an dem das Bright White Be
