Grid Tie Wechselrichter - Gunook

2024 Autor: John Day | [email protected]. Zuletzt bearbeitet: 2024-01-30 07:17

Dies ist ein fleischiges Projekt, also schnallen Sie sich an!

Grid Tie-Wechselrichter ermöglichen es Ihnen, Strom in eine Netzsteckdose zu stecken, was eine großartige Fähigkeit ist. Ich finde die Leistungselektronik und die Steuerungssysteme interessant, die an ihrem Design beteiligt sind, also habe ich meine eigenen gebaut. Dieser Bericht teilt, was ich gelernt habe und dokumentiert, wie ich die Dinge gemacht habe. Ich wäre an Ihren Kommentaren interessiert (außer denen, dass Sie nicht mit dem Stromnetz herumspielen).

Alle Konzepte sind skalierbar, aber dieses Setup hatte eine maximale Leistung von 40 Watt, bevor die Filterinduktivitäten zu sättigen begannen. Der Ausgangsstrom war sinusförmig mit THD < 5%.

Sehen Sie sich die Software auf meinem GitHub an

Lieferungen

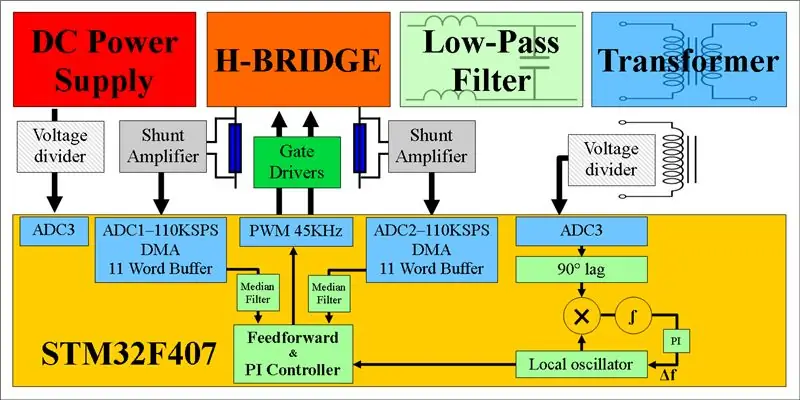
• Ich habe das STM32F407-Entwicklungsboard verwendet. Es läuft mit 168 MHz und verfügt über 3 integrierte ADCs mit einer Auflösung von 12 Bit bei jeweils über 2,4 MSPS (Million Samples Per Second). Das ist verrückt!
• Ich habe das Entwicklungsboard DRV8301 verwendet. Dieser beherbergt eine 60-V-H-Brücke zusammen mit den erforderlichen Gate-Treibern, Strom-Shunts und Strom-Shunt-Verstärkern. Super nett!
• Ich habe einen 230-25V Ringkerntransformator mit 2 Ausgangsabgriffen verwendet. Das bedeutete, dass ich nicht direkt Netzspannung erzeugen musste, sondern stattdessen mit Spitzenspannungen von 40 Volt arbeiten konnte. Viel sicherer!
• Ich habe eine Last von Induktivitäten und Kondensatoren zusammengeschaltet, um die L- und C-Werte zu erhalten, die ich für den Filter wollte.
• Ein Oszilloskop und ein Differenzialtastkopf sind der Schlüssel für ein Projekt wie dieses. Ich habe ein Picoskop

Schritt 1: Was ist Netzstrom?

Was Sie an einer Steckdose (in Großbritannien) erhalten, ist ein Sinussignal mit 50 Hz 230 V RMS mit einer sehr niedrigen Impedanz. Dazu ein paar Dinge:

50Hz - Die Netzfrequenz wird sehr genau auf 50Hz gehalten. Es variiert leicht, aber in 90% der Fälle liegt es zwischen 49,9 und 50,1 Hz. Siehe hier. Sie können sich vorstellen, wie sich all die riesigen Generatoren in Kraftwerken im ganzen Land im Gleichklang drehen. Sie rotieren synchron und erzeugen für uns ein 50Hz Sinussignal. Ihre kombinierte massive Rotationsträgheit braucht Zeit, um zu verlangsamen oder zu beschleunigen.

Theoretisch würde eine riesige Last an das Stromnetz die Generatoren des Landes verlangsamen. Als Reaktion darauf forderten die Jungs im Kontrollbüro des National Grid jedoch Kraftwerke auf, ihre Kessel zu befeuern, die Wärme hochzudrehen und diese Generatoren stärker zu zwingen, mit der Nachfrage Schritt zu halten. Angebot und Nachfrage stehen somit in einem ständigen Tanz miteinander.

Noch etwas zum 50Hz Signal. Obwohl sie um 50 Hz sehr leicht schwankt, stellen die Jungs an der Spitze sicher, dass die durchschnittliche Frequenz über den Tag genau 50 Hz beträgt. Wenn das Raster also 10 Minuten lang bei 49,95 Hz liegt, stellen sie sicher, dass es später bei 50,05 Hz läuft, um die genaue Anzahl der Zyklen auf 50 Hz x 60 Sekunden x 60 Minuten x 24 Stunden = 4, 320, 000 / Tag zu bringen. Sie tun dies genau mit der Internationalen Atomzeit. Haushalts-, Büro- und Industriegeräte können somit die Netzfrequenz nutzen, um die Zeit zu halten. Dies geschieht beispielsweise häufig bei mechanischen Steckdosen-Timern.

230V - Dies ist die RMS-Spannung (Root Mean Square) des 50-Hz-Signals. Das tatsächliche Signal schwingt bis zu einer Spitze von 325 V. Dies ist wichtig zu wissen, denn wenn Sie einen Wechselrichter bauen, müssen Sie so hohe Spannungen erzeugen, damit Strom in die Stecker fließt.

In Wirklichkeit sind die Spannungen an einer Steckdose in Ihrem Haus sehr variabel. Das liegt am Spannungsabfall über den Widerstand in Drähten, Steckern, Sicherungen, Transformatoren usw. Widerstand gibt es überall. Wenn Sie eine elektrische Dusche mit 11 Kilowatt (das sind ~ 50 Ampere) einschalten, werden Sie selbst bei einem Widerstand von 0,2 Ohm um 10 Volt abfallen. Sie können dies daran erkennen, dass die Lichter ganz leicht dimmen. Große Motoren, wie zum Beispiel in Staubsaugern, ziehen große Ströme, während der Motor auf Touren kommt. So sieht man beim Einschalten oft ein leichtes Flackern der Lichter.

Mein Punkt ist, dass die Netzspannung viel variabler ist. Hier in Großbritannien sollen es 230 V mit einer Toleranz von +10%/-6% sein. Sie können mit plötzlichen Änderungen und Schwankungen rechnen, wenn große Lasten in der Nähe ein- und ausgeschaltet werden. Denken Sie an Wäschetrockner, Wasserkocher, Öfen, Staubsauger usw.

Sinusförmig - Das Signal sollte eine schöne saubere Sinuswelle sein, aber in Wirklichkeit saugen einige nichtlineare Geräte ihre Leistung an bestimmten Punkten im Sinuswellenzyklus. Dies führt zu Verzerrungen und deshalb ist das Signal keine perfekte Sinuswelle. Nichtlineare Lasten umfassen typischerweise Computernetzteile, Leuchtstoffröhren, Ladegeräte, Fernseher usw.

Total Harmonic Distortion (THD) quantifiziert dies in der Wellenform. Es gibt Vorschriften, wie sauber der Ausgang eines Wechselrichters sein muss. Wenn es nicht in der Lage ist, ein ausreichend sauberes Signal zu erzeugen, wird es nicht zum Verkauf zugelassen. Dies ist wichtig, da der Oberwellengehalt im Netz die Effizienz einiger daran angeschlossener Geräte verringert (insbesondere ungerade Oberwellen). Ich glaube, der maximal zulässige THD beträgt 8%

Niedrige Impedanz – Wenn Sie über einen netzgebundenen Wechselrichter nachdenken, sollten Sie dies berücksichtigen. Es gibt alle Arten von Lasten, die an das Netz angeschlossen sind, einschließlich induktiver, ohmscher und gelegentlich kapazitiver Lasten. Die Impedanz ist also unbekannt und veränderbar. Der Widerstand ist sehr klein, d.h. wenn Sie eine hohe Stromlast anschließen, sinkt die Spannung überhaupt nicht.

Schritt 2: So drücken Sie Strom in das Netz

Um Strom in das Netz einzuspeisen, müssen wir ein Signal synthetisieren, das genau der Frequenz und Phase des Netzes entspricht, jedoch mit einer geringfügig höheren Spannung.

Aufgrund des geringen Widerstands des Gitters ist es schwierig genau zu wissen, um wie viel diese Spannung erhöht werden muss. Und da die RMS-Spannung schwankt, müssen wir sicherstellen, dass wir mit ihr schwanken. Nur ein festes 50-Hz-Spannungssignal zu erzeugen, das etwas höher als die Netzspannung ist, wird nicht funktionieren!

PI-Regelung des Ausgangsstroms

Was wir brauchen, ist eine Regelschleife, in der wir den Momentanstrom messen, den wir in das Netz einspeisen, und unsere Ausgangsspannung automatisch anpassen, um den gewünschten Strom zu treiben. Dadurch wird unser Ausgang effektiv in eine Stromquelle (und nicht in eine Spannungsquelle) umgewandelt, die zum Ansteuern niedriger Impedanzen besser geeignet ist. Wir können dies erreichen, indem wir einen PI-Regelkreis (Proportional Integral) verwenden:

PI-Regelkreise sind fantastisch! Sie bestehen aus 3 Teilen:

• Der Messwert - Der Strom, den wir ins Netz einspeisen
• Der Sollwert - Der Strom, den wir ins Netz einspeisen wollen
• Der Ausgang - Die zu erzeugende Signalspannung

Bei jedem Aufruf des PID-Algorithmus übergeben wir die aktuellste Strommessung und den gewünschten Sollwert. Es wird eine beliebige Zahl zurückgegeben (proportional zur zu erzeugenden Ausgangsspannung).

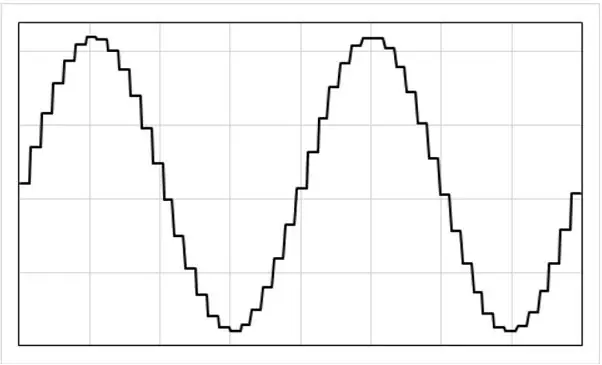
Unser PID-Regelalgorithmus ermöglicht es uns, den gewünschten Ausgangsstrom zu jedem Zeitpunkt zu wählen. Um einen sinusförmigen Ausgangsstrom von 50 Hz zu erzeugen, müssen wir unseren angeforderten Strom kontinuierlich sinusförmig ändern.

Der PID-Algorithmus wird alle 100 us aufgerufen (entspricht 200 Mal pro 50 Hz-Zyklus). Es ist bei jedem Aufruf in der Lage, direkt die Ausgangsspannung und damit indirekt den Ausgangsstrom anzupassen. Als Ergebnis erzeugen wir einen abgestuften Stromausgang ähnlich dem im Bild gezeigten, wobei jeder Schritt alle 100 us auftritt. Das bietet genügend Auflösung.

Vorsteuerung

Wir können die Arbeitslast des PI-Reglers massiv reduzieren, indem wir auch einen Feedforward-Regler hinzufügen. Das ist einfach! Wir kennen die ungefähre Ausgangsspannung, die wir erzeugen müssen (entspricht der momentanen Netzspannung). Der PI-Regler kann dann die winzige zusätzliche Spannung hinzufügen, die zum Antreiben eines Ausgangsstroms benötigt wird.

Der Feedforward-Regler passt die Ausgangsspannung des Wechselrichters selbst an die Netzspannung an. Es sollte kein Strom fließen, wenn wir gut genug zusammenpassen. Die Feedforward-Steuerung übernimmt daher 99% der Output-Steuerung.

Aufgrund des geringen Widerstands des Netzes würde jede Differenz zwischen unserer FF-Ausgangsspannung und der Netzspannung zu einem großen Strom führen. Ich habe daher einen Pufferwiderstand von 1 Ohm zwischen Wechselrichter und Netz hinzugefügt. Dies führt zwar zu Verlusten, aber sie sind im Großen und Ganzen recht klein.

Schritt 3: Erzeugung der Ausgangsspannung mit PWM

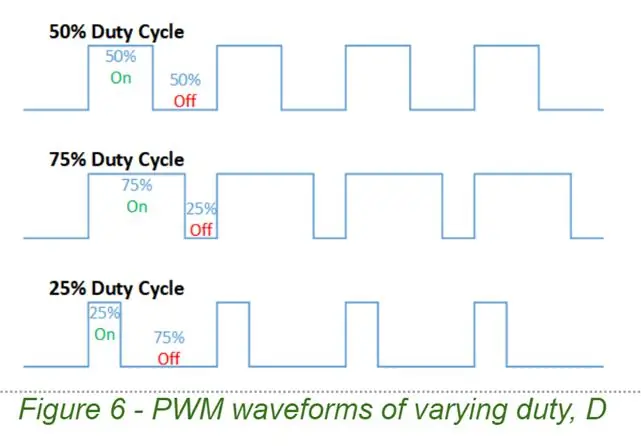
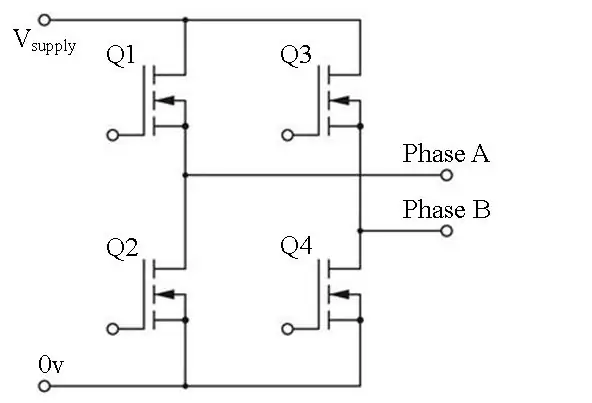
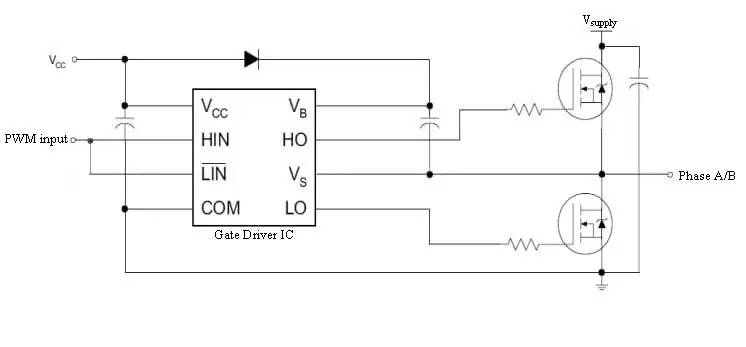
Obwohl wir den Ausgangsstrom indirekt steuern, ist es eine Ausgangsspannung, die wir zu einem bestimmten Zeitpunkt erzeugen. Wir verwenden PWM (Pulsweitenmodulation), um unsere Ausgangsspannung zu erzeugen. PWM-Signale können problemlos von Mikrocontrollern erzeugt und mit einer H-Brücke verstärkt werden. Es handelt sich um einfache Wellenformen, die durch 2 Parameter gekennzeichnet sind, die Frequenz F und das Tastverhältnis D.

Eine PWM-Wellenform schaltet zwischen 2 Spannungen um, in unserem Fall 0V und Vsupply

• Bei D = 1,0 ist die PWM-Wellenform einfach DC bei Vsupply
• Mit D = 0,5 erhalten wir eine Rechteckwelle mit einer durchschnittlichen Spannung von 0,5 x Vsupply, (dh D x Vsupply)
• Mit D = 0,1 erhalten wir eine gepulste Wellenform mit einem Periodenmittel von 0,1 x Vsupply
• Bei D = 0.0 ist der Ausgang eine Flatline (DC bei 0v)

Die durchschnittliche Spannung ist der Schlüssel. Mit einem Tiefpassfilter können wir alles außer der DC-Durchschnittskomponente entfernen. Durch Variieren des PWM-Tastverhältnisses D können wir jede gewünschte Gleichspannung herstellen. Süss!

Einsatz einer H-Brücke

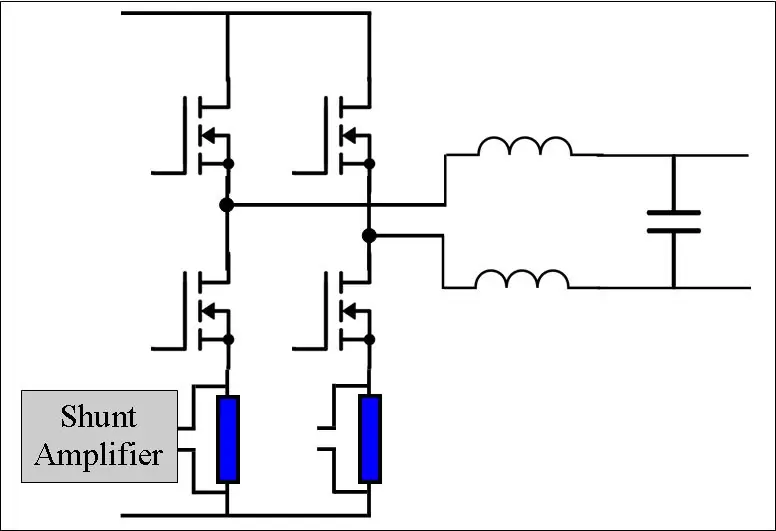
Eine H-Brücke besteht aus 4 Schaltelementen. Dies können BJTs, MOSFETs oder IGBTs sein. Um die erste Hälfte (0 - 180 Grad) der Sinuswelle zu erzeugen, setzen wir Phase B niedrig, indem wir Q3 aus- und Q4 einschalten (dh PWM mit D = 0 anwenden). Dann führen wir unser PWMing auf Phase A durch. Für die zweite Hälfte, in der VAB negativ ist, setzen wir Phase A niedrig und wenden unsere PWM an Phase B an. Dies wird als bipolares Schalten bezeichnet.

Die MOSFETs in der H-Brücke müssen von einem Gate-Treiber angesteuert werden. Dies ist ein eigenes Thema, aber ein einfacher Chip kann sich darum kümmern. Das DRV8301-Entwicklungsboard beherbergt bequem die H-Brücke, Gate-Treiber und Strom-Shunts für uns, was dieses Projekt viel einfacher macht.

Schritt 4: Strom messen

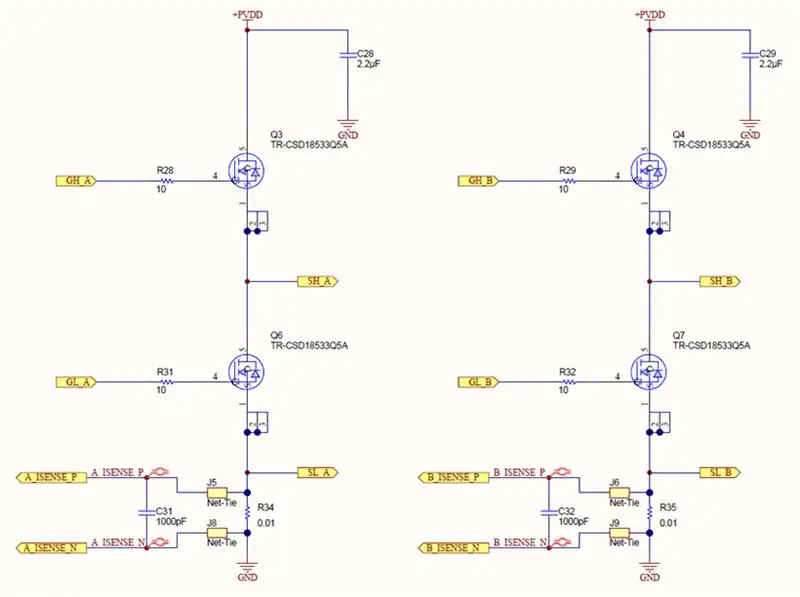
Jeder Zweig der H-Brücke hat einen Shunt-Widerstand und einen Differenzverstärker. Unsere Shunts sind 0,01 Ohm und unsere Verstärker sind auf eine Verstärkung von 40 eingestellt. Daher entwickelt 1 Ampere 10 mV über den Shunt, der anschließend auf 400 mV verstärkt wird.

Die Ausgänge der Shunt-Verstärker werden von den 12-Bit-ADCs des STM32F407 gelesen, die im kontinuierlichen Konvertierungsmodus laufen. Die ADCs sind so eingestellt, dass sie jeden Shunt mit 110 KSPS abtasten und der DMA-Controller schreibt die Konvertierungen automatisch in einen 11-Wort-Ringpuffer im RAM. Wenn eine aktuelle Messung gewünscht wird, rufen wir eine Funktion auf, die den Medianwert dieses 11-Wort-Puffers zurückgibt.

Da wir bei jeder PID-Iteration (bei 10KHz) aktuelle Messungen anfordern, aber unsere 11-Wort-ADC-Puffer mit einer Rate von 110KHz füllen, sollten wir bei jeder PID-Iteration völlig neue Daten erhalten. Der Grund für die Verwendung eines Medianfilters liegt darin, dass die PWM-Schaltung Spitzen in den Mix einführen kann und Medianfilter störende ADC-Abtastwerte sehr effektiv beseitigen.

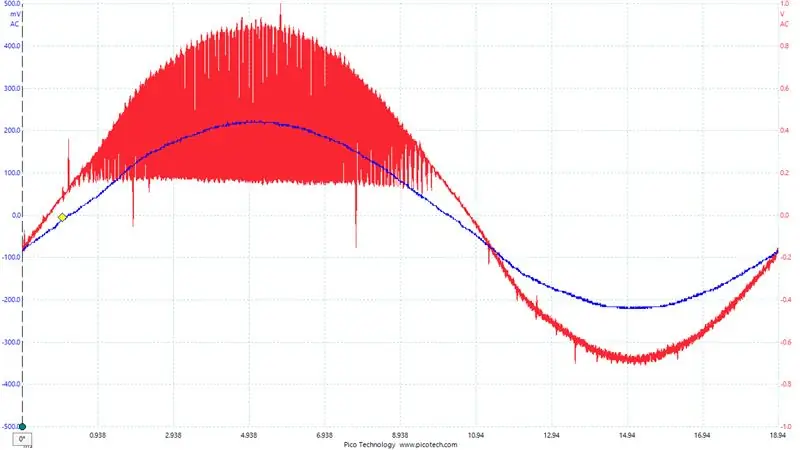
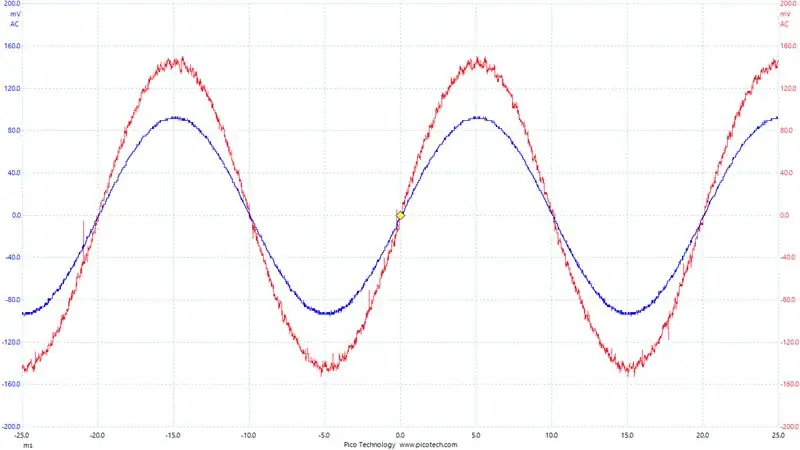
Ein wichtiger Punkt hier: Welchen Schenkel der H-Brücke verwenden wir für Strommessungen? Nun, es hängt davon ab, welches Bein wir gerade PWMing und welches gerade niedrig gehalten wird. Das niedrig gehaltene Bein ist dasjenige, von dem wir unseren Strom messen möchten, da auf dieser Seite immer Strom durch den Shunt-Widerstand fließt. Im Vergleich dazu fließt auf der PWM-Seite kein Strom durch den Low-Side-Shunt, wenn der High-Side-MOSFET eingeschaltet und der Low-Side ausgeschaltet ist. Wir ändern also, an welchem Zweig wir den Strom messen, basierend auf der Ausgangspolarität des Wechselrichters. Sie können dies deutlich im Bild sehen, das den Ausgang eines der Shunt-Verstärker über einen bestimmten Zeitraum zeigt. Natürlich wollen wir während des glatten Bits Messungen vornehmen.

Um zu helfen, unsere aktuellen Messwerte zu debuggen. Den Digital-Analog-Wandler habe ich auf dem STM32F407 eingerichtet. Ich schrieb die aktuellen Messwerte, die ich erhielt, und bereicherte die Ausgabe. Sie können dies im letzten Bild sehen, das Blau ist die Spannung am Ausgangspufferwiderstand (dh der Ausgangsstrom / 1,1 Ohm) und das rote Signal ist unser DAC-Ausgang.

Schritt 5: Filtern der Ausgabe

Der Ausgangsfilter ist ein wichtiger Bestandteil des Designs. Wir brauchen diese Eigenschaften daraus:

1. Blockieren Sie alle Hochfrequenzschaltungen, lassen Sie jedoch ein 50-Hz-Signal durch
2. Geringe Verluste
3. Nicht zu resonieren!
4. Um mit den auftretenden Strömen und Spannungen fertig zu werden

Die Fourier-Transformation eines PWM-Signals der Frequenz F, Tastverhältnis D, zwischen 0 - Vsupply Volt ist: (D x Vsupply) + Sinuswellen bei der Grundfrequenz F und Harmonische danach

Das ist brilliant! Das heißt, wenn wir unser PWM-Signal durch einen Tiefpassfilter schicken, der die PWM-Grundwelle und alles darüber blockiert. Bleibt nur noch der Gleichspannungsterm. Durch Variieren des Tastverhältnisses können wir leicht jede gewünschte Spannung zwischen 0 - Vsupply erzeugen, wie erklärt.

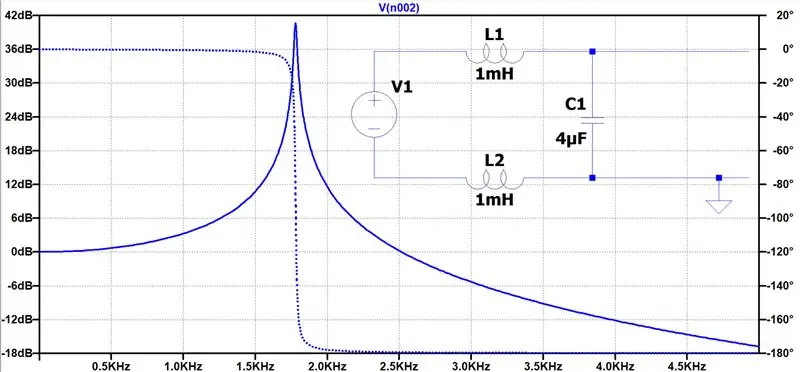
Basierend auf den oben genannten gewünschten Eigenschaften können wir den Ausgangsfilter entwerfen. Wir brauchen einen Tiefpassfilter mit minimalem Widerstand, um Verluste zu vermeiden. Daher verwenden wir nur Induktivitäten und Kondensatoren. Wenn wir eine Resonanzfrequenz zwischen 1 - 2 KHz wählen, vermeiden wir Resonanzen, da wir keine Signale in der Nähe dieser Frequenz einspeisen. Hier ist unser Filterdesign. Wir nehmen unseren Ausgang als die Spannung an C1.

Durch die Wahl von L1 = L2 = 440uH, C1 = 8,4uF berechnen wir eine Resonanzfrequenz von 1,85KHz. Dies sind auch realistische Komponentenwerte.

Es ist wichtig sicherzustellen, dass unsere Induktivitäten nicht bei den von uns erwarteten Strömen in die Sättigung geraten. Die von mir verwendeten Induktivitäten haben einen Sättigungsstrom von 3A. Dies wird der begrenzende Faktor für die Ausgangsleistung unserer Schaltung sein. Die Nennspannung des Kondensators ist ebenfalls wichtig zu berücksichtigen. Ich verwende 450-V-Keramik, was in diesem Fall sehr übertrieben ist!

Der Bode-Plot (für leicht unterschiedliche L/C-Werte) wurde mit LTspice erstellt. Es zeigt uns die Dämpfung, die verschiedenen Eingangsfrequenzen zugefügt wird. Wir können die Resonanzfrequenz bei 1,8 KHz deutlich sehen. Es zeigt, dass ein 50-Hz-Signal fast vollständig unverfälscht ist, während ich Ihnen sagen kann, dass ein 45-KHz-Signal um 54 dB gedämpft wird!

Wählen wir also unsere PWM-Trägerfrequenz von ~45KHz. Durch die Wahl höherer PWM-Trägerfrequenzen kann die Filterfrequenz erhöht werden. Das ist gut, weil es die L- und C-Werte kleiner macht. Das bedeutet kleinere und billigere Komponenten. Der Nachteil ist, dass höhere PWM-Schaltfrequenzen größere Verluste in den Transistorschaltern mit sich bringen.

Schritt 6: Synchronisieren von Phase und Frequenz

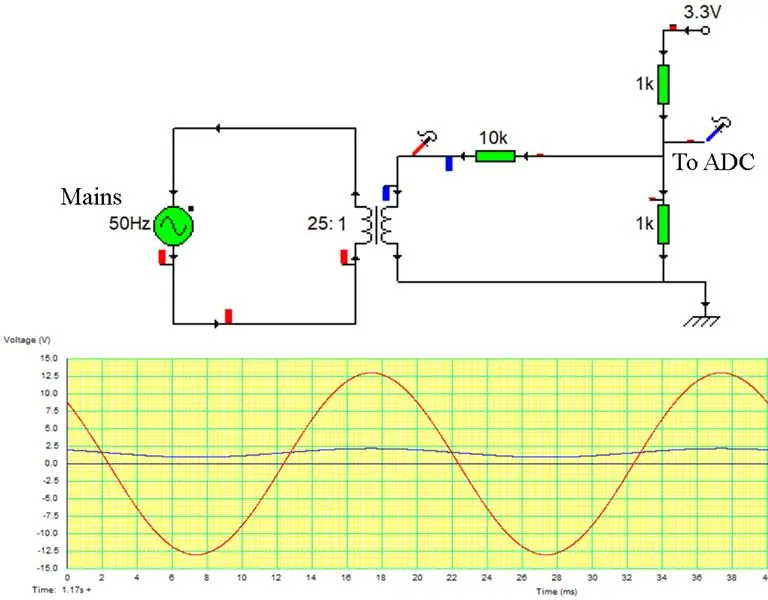
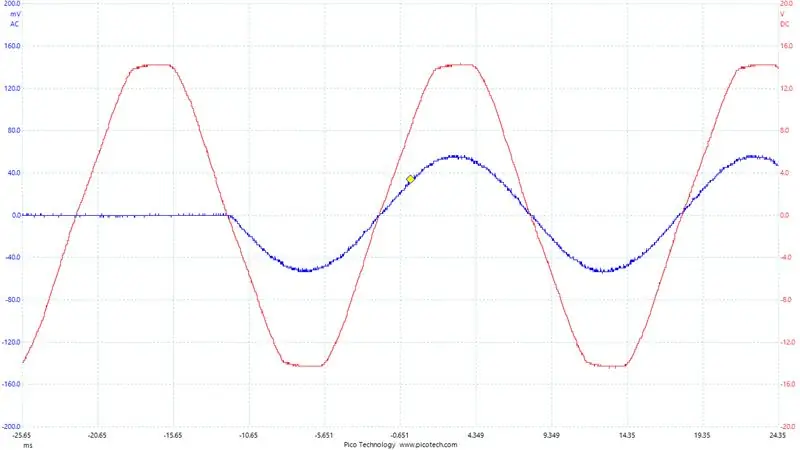
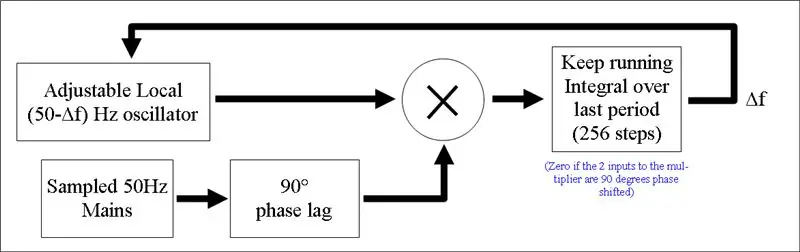
Die Synchronisierung auf die Netzphase und -frequenz macht einen netzgebundenen Wechselrichter aus. Wir verwenden eine digitale Implementierung einer PLL (Phase Locked Loop), um eine genaue Phasennachführung des Netzsignals zu erreichen. Wir tun dies durch:

1. Abtasten der Netzspannung
2. Eigenes lokales 50Hz-Sinussignal erzeugen
3. Vergleich der Phase zwischen unserem lokalen Signal und dem Netzsignal
4. Anpassen der Frequenz des lokalen Signals, bis die Phasendifferenz zwischen den 2 Signalen Null ist

1) Abtasten der Netzspannung

Wir konfigurieren einen 3. ADC-Kanal zum Lesen der Netzspannung. Dies erhalten wir durch Spannungsteilung eines Transformatorabgriffs wie gezeigt. Dies liefert eine skalierte Spannung von etwa 1,65 V, die genau die Netzspannung repräsentiert.

2) Erzeugen eines lokalen 50-Hz-Sinussignals Die Erzeugung unserer eigenen lokalen 50-Hz-Sinuswelle ist einfach. Wir speichern eine Nachschlagetabelle mit 256 Sinuswerten. Unser simulierter Sinuswert lässt sich leicht mithilfe eines Nachschlageindex ermitteln, der inkrementell durch die Tabelle rotiert.

Wir müssen unseren Index mit genau der richtigen Rate erhöhen, um ein 50-Hz-Signal zu erhalten. Nämlich 256 x 50Hz = 12.800/s. Wir tun dies, indem wir Timer9 verwenden, der mit 168 MHz getaktet ist. Indem wir 168MHz/12800 = 13125 Takt-Ticks warten, werden wir unseren Index mit der richtigen Rate stufen.

3) Vergleich der Phase zwischen unserem lokalen Signal und dem NetzsignalDas ist der coole Teil! Wenn Sie das Produkt von cos(wt) x sin(wt) über 1 Periode integrieren, ist das Ergebnis null. Wenn die Phasendifferenz etwas anderes als 90 Grad beträgt, erhalten Sie eine Zahl ungleich Null. Mathematisch:

Integral[Asin(t) x Bsin(t + φ)] = Ccos(φ)

Das ist toll! Es ermöglicht uns, das Netzsignal sin(ωt) mit unserem lokalen Signal sin(⍵t + φ) zu vergleichen und einen Wert zu erhalten.

Es gibt jedoch ein Problem, das angegangen werden muss: Wenn wir möchten, dass unsere Signale in Phase bleiben, müssen wir unsere lokale Frequenz anpassen, um den Ccos(φ)-Term maximal zu halten. Dies wird nicht sehr gut funktionieren und wir werden eine schlechte Phasenverfolgung bekommen. Dies liegt daran, dass d/dφ von ɑcos(φ) 0 bei φ = 0 ist. Dies bedeutet, dass der Ccos(φ)-Term bei Phasenänderungen nicht sehr stark variiert. Ist das sinnvoll?

Es wäre viel besser, das abgetastete Netzsignal um 90 Grad zu verschieben, damit es zu cos(ωt + φ) wird. Dann haben wir das:

Integral[Asin(t) Bcos(t + φ)] = Csin(φ)

Die Einführung einer 90-Grad-Phasenverschiebung ist einfach, wir fügen einfach unsere Netz-ADC-Spannungsproben in ein Ende eines Puffers ein und nehmen sie eine Reihe von Proben später heraus, was einer Phasenverschiebung von 90 Grad entspricht. Da die Netzfrequenz kaum von 50 Hz abweicht, funktioniert eine einfache Zeitverzögerungstechnik hervorragend.

Wir multiplizieren nun unser um 90 Grad phasenverschobenes Netzsignal mit unserem lokalen Signal und führen ein laufendes Integral des Produkts über die letzte Periode (dh über die letzten 256 Werte).

Das uns bekannte Ergebnis ist Null, wenn die beiden Signale genau 90 Grad auseinander gehalten werden. Das ist fantastisch, weil es die Phasenverschiebung, die wir gerade auf das Netzsignal angewendet haben, rückgängig macht. Nur zur Verdeutlichung, anstatt den Integralterm zu maximieren, versuchen wir, ihn Null zu halten und wir phasenverschieben unser Netzsignal. Die durch diese beiden Änderungen eingeführten 90-Grad-Phasenverschiebungen heben sich gegenseitig auf.

Wenn also Integral_Result < 0 ist, wissen wir, dass wir unsere Lokaloszillatorfrequenz erhöhen müssen, um sie wieder in Phase mit dem Netz zu bringen und umgekehrt.

4) Einstellen der Frequenz des lokalen SignalsDieses Bit ist einfach. Wir passen einfach den Zeitraum zwischen der Erhöhung durch unseren Index an. Wir schränken ein, wie schnell wir die Phasendifferenz korrigieren können, indem wir im Wesentlichen Störeinflüsse herausfiltern. Wir tun dies mit einem PI-Regler mit einem sehr kleinen I-Anteil.

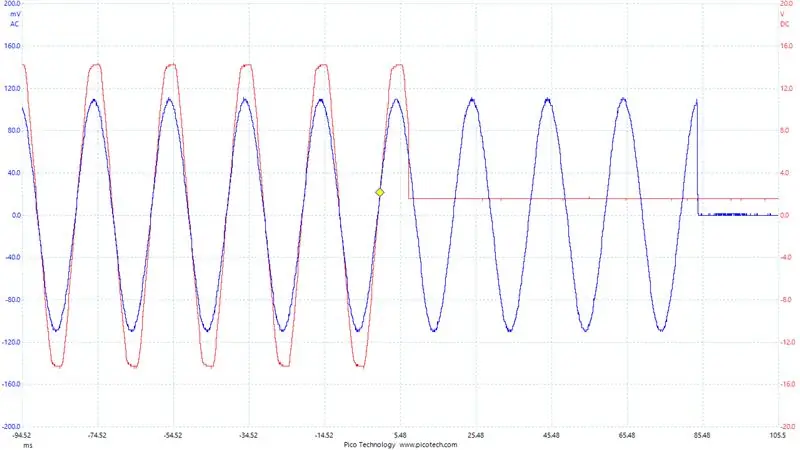
Und das ist es. Wir haben unseren lokalen Sinuswellenoszillator (der den Ausgangsstromsollwert einstellt) so eingestellt, dass er mit der Netzspannung in Phase ist. Wir haben einen PLL-Algorithmus implementiert und er funktioniert wie ein Traum!

Die Erhöhung der Frequenz unseres Lokaloszillators verringert auch die Phasenverschiebung des Netzsignals. Da wir die Frequenzanpassung auf +/-131 Ticks (+/- ~1%) beschränken, beeinflussen wir die Phasenverschiebung um maximal +/- 1°. Dies spielt keine Rolle, während sich die Phasen synchronisieren.

Theoretisch würden wir unsere Phasenverriegelung verlieren, wenn die Netzfrequenz um mehr als 0,5 Hz abweicht. Dies liegt an unserer obigen Einschränkung, wie stark wir unsere Lokaloszillatorfrequenz anpassen können. Dies wird jedoch nicht passieren, es sei denn, das Netz droht zu versagen. Unser Anti-Islanding-Schutz wird an dieser Stelle sowieso greifen.

Wir führen beim Start eine Nulldurchgangserkennung durch, um unser Bestes zu versuchen, die Signale gleichphasig vom Offset aus zu starten.

Schritt 7: Anti-Islanding

Wikipedia hat einen großartigen Artikel über Islanding- und Anti-Islanding-Techniken. Es impliziert auch, dass die Leute mehr als nötig zischen und flattern, wenn es um dieses Thema geht. "Oh, Sie können keinen eigenen Wechselrichter bauen, Sie werden jemanden töten usw.."

Wie der Wikipedia-Artikel besser erklärt, wenden wir ein paar Sicherheitsvorkehrungen an, die zusammen einen ausreichenden Schutz bieten (meiner Meinung nach):

1. Unter-/Überspannung
2. Unter-/Überfrequenz

Wir können diese Situationen erkennen, indem wir einfach unsere abgetastete skalierte Netzspannung analysieren. Wenn etwas aus dem Ruder läuft, deaktivieren Sie die H-Brücke und warten Sie, bis sich die Dinge wieder normalisieren.