Kennen Sie ESP32 ADC-Anpassung? - Gunook

2024 Autor: John Day | [email protected]. Zuletzt bearbeitet: 2024-01-30 07:19

Heute werde ich über ein eher technisches Problem sprechen, aber eines sollte meiner Meinung nach jeder kennen, der mit ESP32 arbeitet: das Problem der ADC (Analog-Digital-Wandler) Leseanpassung. Das finde ich wichtig, denn bei einer "Messung", insbesondere bei einem Gerät mit Analogausgang, muss man sich absolut sicher sein, dass die Messung richtig durchgeführt wird.

Im heutigen Video werden wir daher Messungen mit dem "Analog-Digital-Wandler" des ESP32 durchführen, die Wandlungsabweichungen beobachten und ein ADC-Abgleich-/Kalibrierungsverfahren anwenden.

Schritt 1: Was ist ein AD-Wandler?

Ein AD-Wandler ist eine Schaltung, die eine analoge (kontinuierliche) Größe in digitale (diskrete) Werte umwandeln kann. Was bedeutet das? Dies bedeutet, dass während digitale Werte nur diskrete Werte annehmen können, die durch die Kombination von Nullen und Einsen gebildet werden, eine analoge Größe jeden Wert innerhalb eines Bereichs annehmen kann. Wenn wir beispielsweise die Spannung einer idealen AA-Zelle gemessen haben, könnten wir jeden Wert zwischen 0 V und 1,5 V finden, da dies eine analoge Größe ist. Der Ausgangszustand einer idealen Lampe darf nur zwei Zustände annehmen (aus oder an), was eine diskrete Größe darstellt. Da Mikrocontroller mit dieser diskreten Logik arbeiten, benötigen wir eine Schaltung, die eine analoge Größe in eine digitale (oder diskrete) umwandeln kann.

Schritt 2: Verwendete Ressourcen

• Eine Lolin32 Lite-Karte v1.0.0

• Ein Tektronix TDS1001C-Oszilloskop zur Aufnahme

• Ein USB-Kabel für den ESP32

• Ein Hantek DSO4102C Oszilloskop als Signalgenerator

Schritt 3: ESP32-ADC

Laut Espressif-Daten können die ESP32-Chips in den Messergebnissen einen Unterschied von +/- 6% von einem Chip zum anderen aufweisen.

Außerdem hat die Umrechnung NICHT für jeden verfügbaren Bereich zum Lesen eine lineare Antwort. Espressif bietet eine Methode zur Kalibrierung und schlägt vor, dass Benutzer andere Methoden implementieren, wenn sie dies für erforderlich halten, um die gewünschte Genauigkeit zu erreichen.

Wir führen eine Datenerfassung durch und zeigen daraus die ADC-Antworten und ein Beispiel für die Anwendung eines mathematischen Verfahrens zum Lesen der Anpassung.

Es gibt mehrere (einfache oder komplexere) Möglichkeiten, diese Korrekturen durchzuführen. Es liegt an Ihnen, die für Ihr Projekt am besten geeignete zu evaluieren.

Die hier gezeigte dient der Veranschaulichung und versucht, interessante Punkte anzusprechen, die bei Anpassungen beobachtet werden können.

Schritt 4: Schaltung verwendet

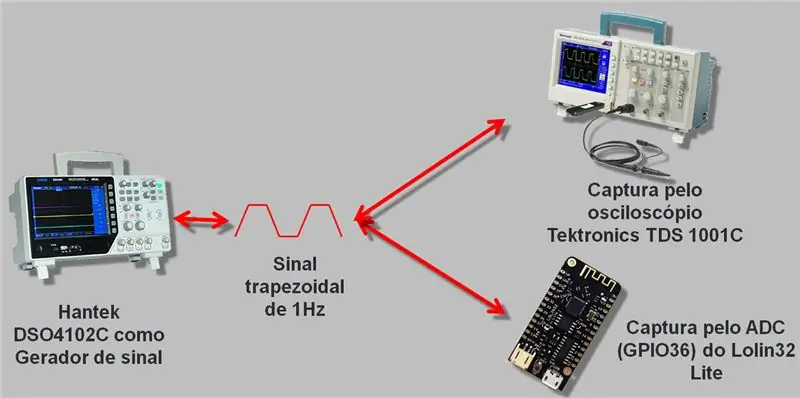
Ich habe ein Oszilloskop mit einem Signalgenerator verwendet, der bis 25 MHz geht, das Hantek DSO4102C. Wir erzeugten eine Welle, die vom ESP A / D und dem Oszilloskop gelesen wurde. Die erhobenen Daten wurden in csv und in einer Tabellenkalkulation erfasst, die ich am Ende des Artikels zum Download überlassen werde.

Schritt 5: Zeichen verwendet

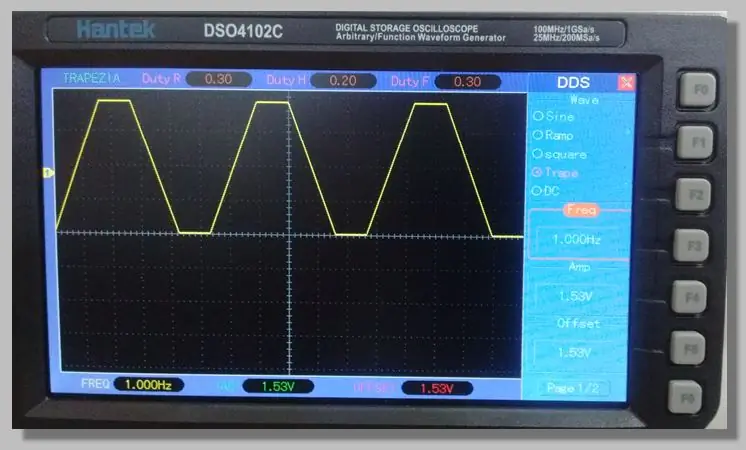
Wir haben uns für ein niederfrequentes Trapezsignal entschieden, das den Zugriff auf die Rampen ermöglicht, die den gesamten Wandlungsbereich durchlaufen. Dies ermöglicht eine große Anzahl von Samples auf diesen Rampen.

Schritt 6: Vom Oszilloskop erhaltene Daten

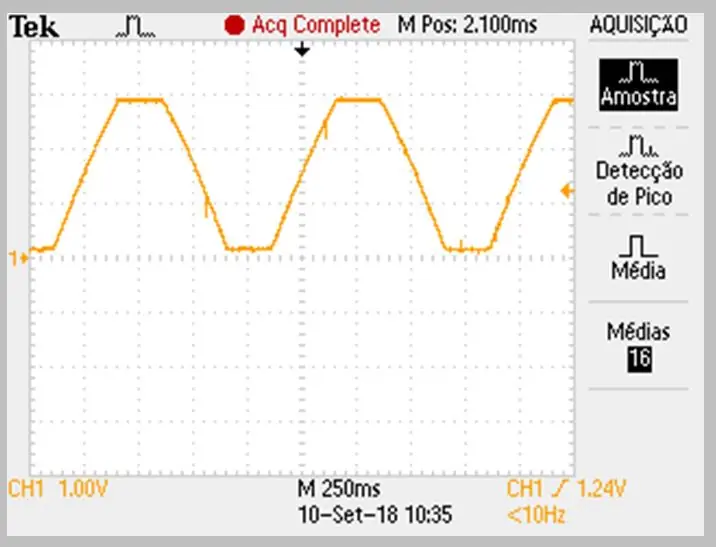
Das Bild der Erfassung wurde durch das Oszilloskop durchgeführt. Die Daten wurden in einer csv-Datei gespeichert. Beachten Sie die leichte Krümmung der steigenden und fallenden Rampen des Signals.

Schritt 7: Vom Oszilloskop erhaltene Daten (csv-Datei in Excel)

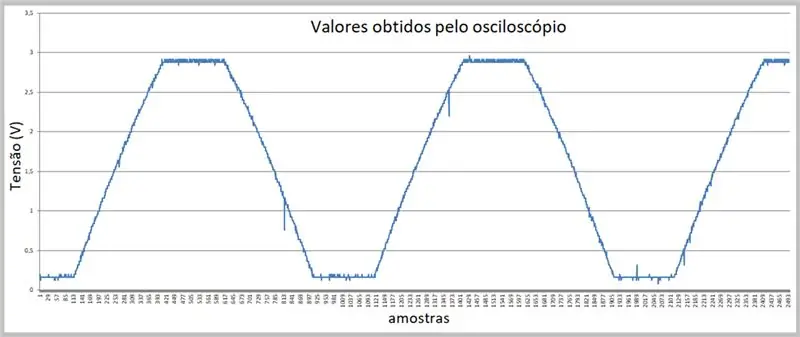
Wir haben die Muster hier.

Schritt 8: Vom ADC erhaltene Daten

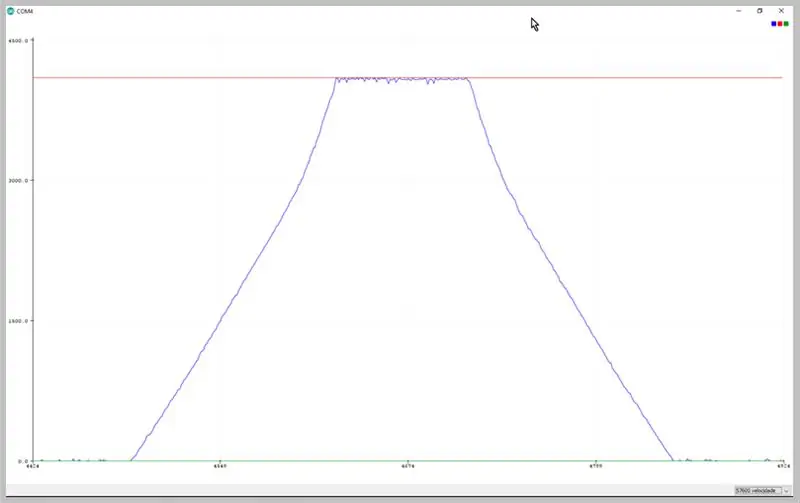
Durch Ändern der Übertragungsrate der seriellen Schnittstelle können wir die vom ADC erfassten Daten anzeigen. Beachten Sie die Verformung des Trapezsignals.

Auf dem seriellen Arduino IDE-Plotter beobachtete Daten

Schritt 9: Von ADC erhaltene Daten - Excel

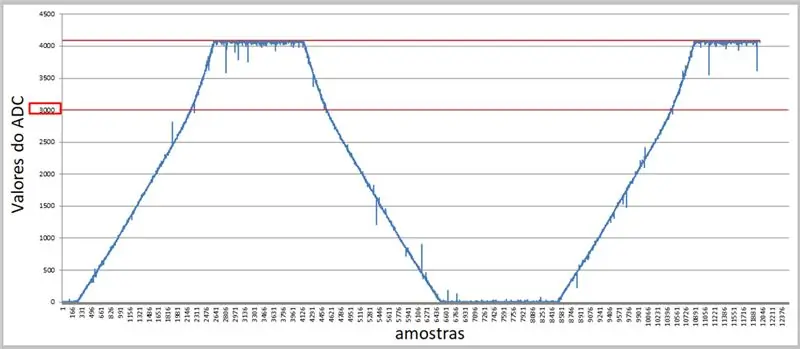
Mit einer höheren Rate und dem seriellen Terminal können wir die Werte erfassen und in Excel für unsere Vergleiche anwenden.

Schritt 10: Vergleich der Steigrampen

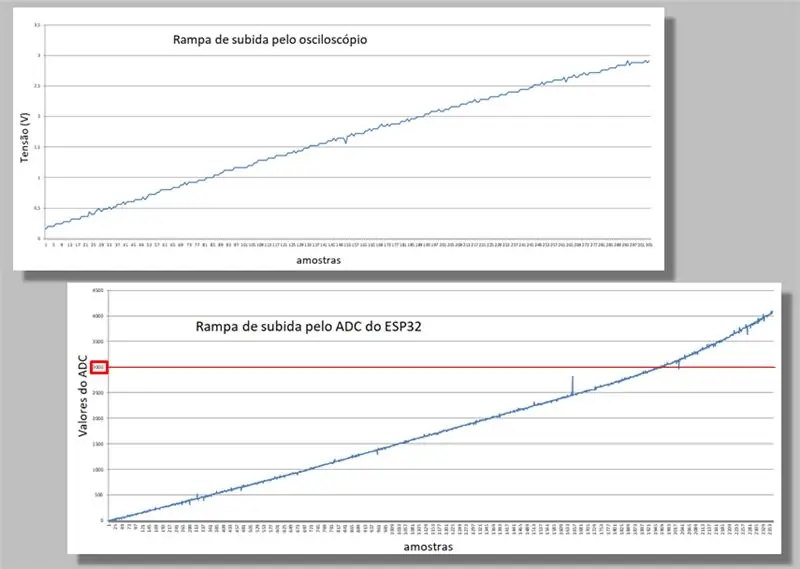
Wir vergleichen die beiden Kletterrampen der beiden Fänge.

Beachten Sie die Krümmung, die an beiden Rampen auftritt.

Beachten Sie auch, dass wir für dieselbe Rampe viel mehr Samples des ESP32 als vom Oszilloskop haben.

Schritt 11: Gleichen der Anzahl der Proben

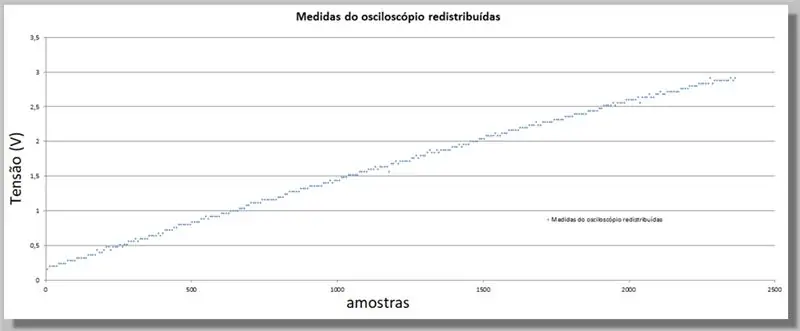
Da der ESP32 eine größere Anzahl von Abtastwerten lieferte als das Oszilloskop, müssen wir diese Werte gleichsetzen, da sie als Index zum Vergleich der beiden Kurven dienen.

Dazu machen wir einen direkten Vergleich.

Wir haben 305 Samples für die Oszilloskop-Rampe und 2365 Samples für die ADC-Rampe.

Da die Rampen den gleichen Bereich haben, können wir sagen, dass wir für jedes Oszilloskop ungefähr 7,75 Abtastungen des ADC haben.

Die Multiplikation des Index jedes Oszilloskop-Abtastwerts ergibt dieselbe Kurve, jedoch mit Indizes, die dem ADC und den neu verteilten Daten entsprechen.

Um die fehlenden Daten für die neuen Positionen zu ergänzen, wenden wir eine Kurve an, die statistisch zu den bekannten Daten passt.

Schritt 12: Füllen der Lücken - Trendlinie

Durch Auswahl der bekannten Daten (blaue Punkte), durch Anklicken und anschließendes Klicken mit der rechten Maustaste wählen wir: "Trendlinie hinzufügen …"

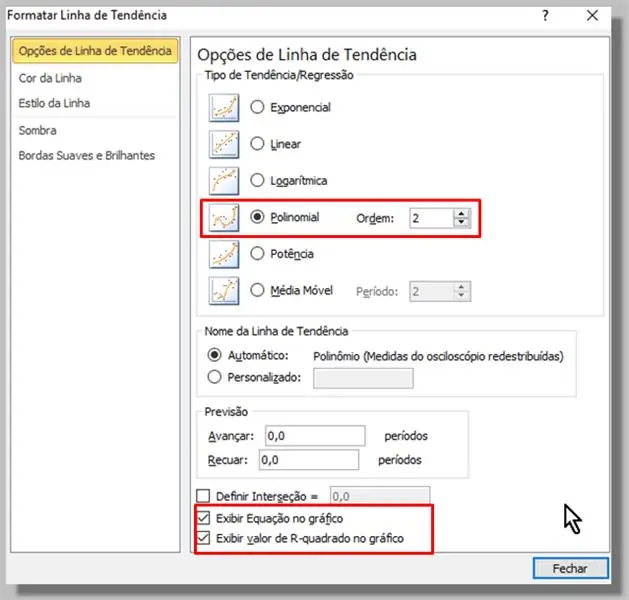
Im erscheinenden Fenster wählen wir den Typ Polynom (Ordnung 2 reicht aus).

Wir haben auch die Optionen "Gleichung im Diagramm anzeigen" und "R-Quadrat-Wert im Diagramm anzeigen" überprüft.

Wir klicken auf "Schließen".

Schritt 13: Füllen der Lücken - Polynomkurve Grad 2

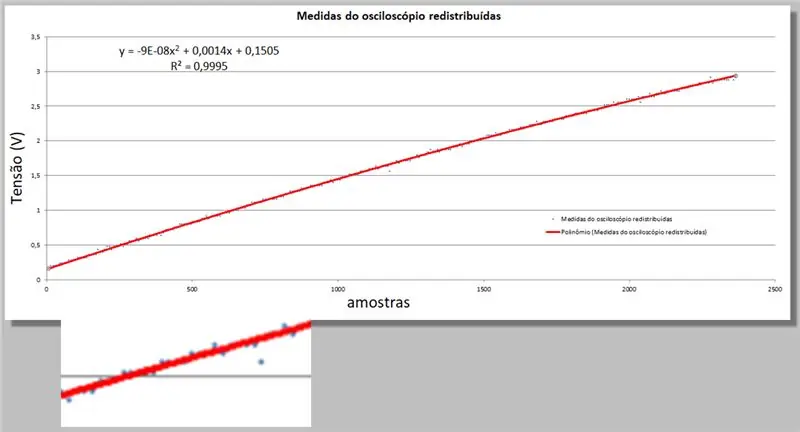
Excel liefert uns zwei neue Informationen; die Gleichung zweiter Ordnung, die am besten zu den Daten passt, und die R-Quadrat-Gleichung, die diese Angemessenheit quantifiziert.

Denken Sie daran, dass die Gleichung umso passender ist, je näher an 1 ist.

Lassen Sie uns nicht in die Mathematik eintauchen, sondern verwenden wir sie einfach als Werkzeug.

Schritt 14: Füllen der Lücken - Auswerten der Funktion

Füllen wir die Stichprobenlücken mit den durch die Gleichung generierten Daten. Und dann vergleiche sie Punkt für Punkt.

y = -9E-08x2 + 0,0014x + 0, 1505

R² = 0, 9999

Oszilloskopspannung = -9E-08 * Index2 + 0,0014 * Index + 0, 1505

Schritt 15: Umwandeln der Oszilloskopspannung in einen äquivalenten Wert zum Vergleich mit dem ADC

Nutzen wir dies, um auch den Wert der Oszilloskopspannung in einen äquivalenten ADC-Wert umzuwandeln.

Da der höchste im ADP des ESP32 erhaltene Wert 4095 war, was dem Messwert von 2,958 V für den gleichen Index entspricht, können wir Folgendes sagen:

Jedes Volt in den Messungen des Oszilloskops entspricht ungefähr 1384,4 Einheiten des AD. Daher können wir alle Messungen des Oszilloskops mit diesem Wert multiplizieren.

Schritt 16: Vergleich der beiden erhaltenen Rampen

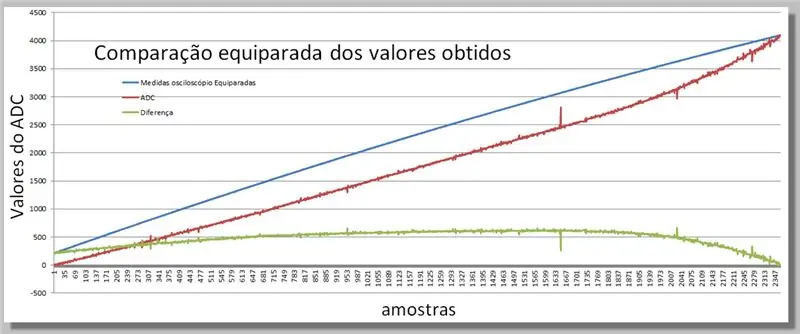
Visualisierung der Unterschiede, die in den beiden Ablesungen erhalten wurden.

Schritt 17: Verhalten der ADC-Lesedifferenz (ERROR)

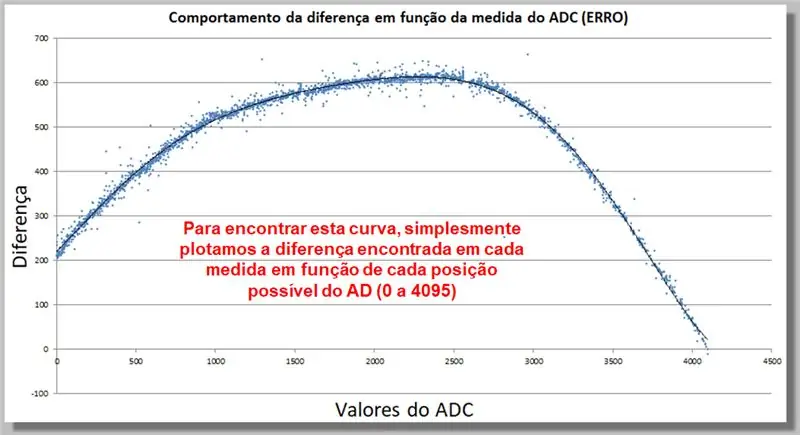
Die folgende Kurve zeigt, wie sich die Differenz der ADC-Messwerte als Funktion der Messung verhält. Diese Datenerhebung ermöglicht es uns, eine Korrekturfunktion zu finden.

Um diese Kurve zu finden, zeichnen wir einfach die in jedem Maß gefundene Differenz als Funktion jeder möglichen AD-Position (0 bis 4095) auf.

Schritt 18: ADC-Lesedifferenzverhalten - Finden einer Korrekturfunktion

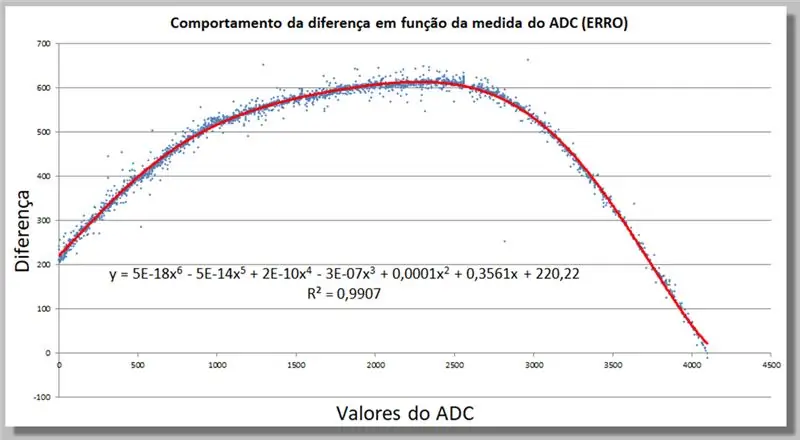
Wir können in Excel eine Korrekturfunktion bestimmen, indem wir eine Trendlinie, jetzt höheren Grades, hinzufügen, bis sie ausreichend mit unseren Daten übereinstimmt.

Schritt 19: Andere Software verwenden

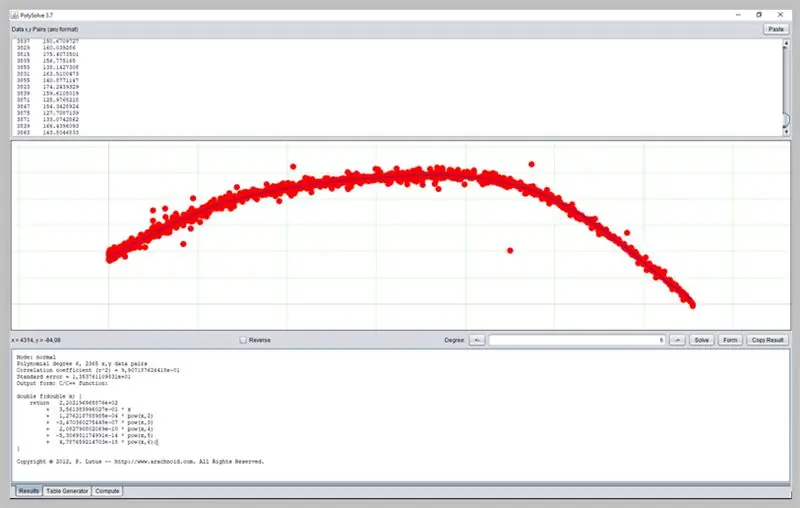
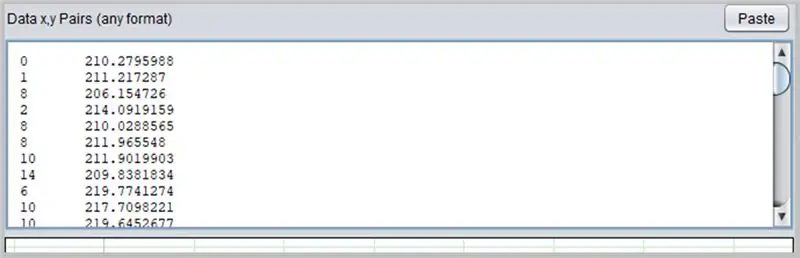
Eine weitere interessante Software zur Kurvenbestimmung ist PolySolve, die direkt unter dem Link: https://arachnoid.com/polysolve/ genutzt oder als Java-Anwendung heruntergeladen werden kann.

Es ermöglicht die Anwendung von polynomialen Regressionen höheren Grades und die Bereitstellung der formatierten Funktion sowie anderer Funktionalitäten.

Um es zu verwenden, geben Sie einfach die Daten in das erste Textfeld ein. Die Daten müssen der Reihenfolge X, Y, getrennt durch ein Komma oder Tabulator, folgen. Seien Sie vorsichtig, wenn Sie den Punkt richtig als Dezimalpunkt verwenden.

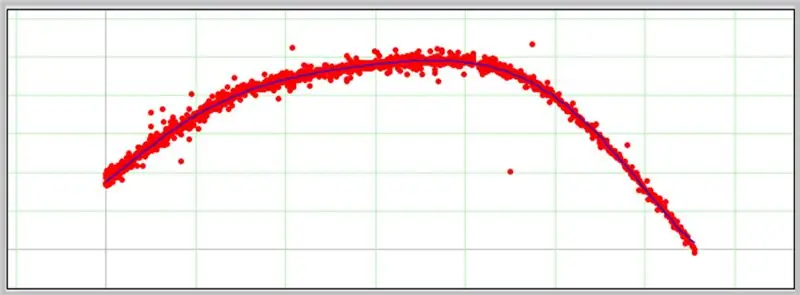
Im nächsten Feld wird ein Diagramm angezeigt, wenn die eingegebenen Daten richtig formatiert sind.

So verlief unsere ADC-Fehlerkurve.

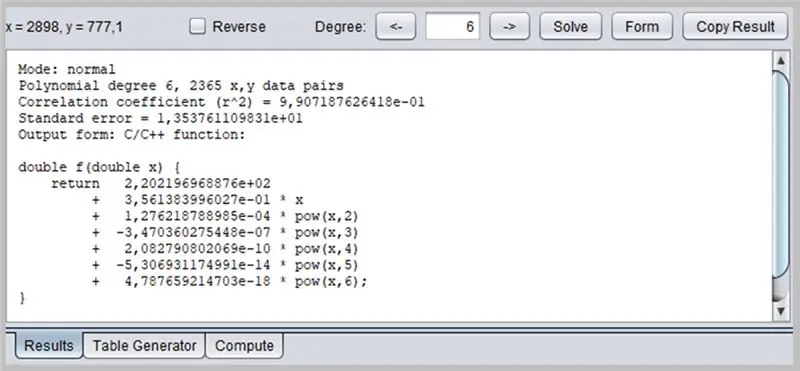
Dieses Fenster präsentiert das Ergebnis der Regression, einschließlich der Funktionsadäquanzdaten, deren Ausgabe wiederum auf verschiedene Weise formatiert werden kann: als C / C ++-Funktion, eine Liste von Koeffizienten, eine in Java geschriebene Funktion usw.

Hinweis: Dezimaltrennzeichen beachten

Schritt 20: Konstanten und Setup ()

Ich weise hier auf den GPIO hin, der für die analoge Erfassung verwendet wird. Ich initialisiere den seriellen Port, sowie den für die analoge Erfassung bestimmten Pin.

const int pin_leitura = 36; // GPIO usado para captura analógica void setup () {Serial.begin (1000000); //Iniciciando a porta serial somente para debug pinMode (pin_leitura, INPUT); //Pino utilizado para captura analógica}

Schritt 21: Loop () und die Korrekturfunktion

Wir erfassen die eingestellte Spannung und drucken die Werte mit oder ohne die richtigen Korrekturen.

Void Schleife () { Int valor_analogico = analogRead (pin_leitura); //realiza a captura da tensão ajustada //Serial.print (valor_analogico + f(valor_analogico)); // imprime os valores para debug (COM CORREÇÃO) Serial.print (valor_analogico); // imprimime os valores para debug (SEM CORREÇÃO) Serial.print (", "); Serial.print (4095); // cria uma linha para marcar o valor máximo de 4095 Serial.print (", "); Serial.println(0); //cria uma linha para marcar o valor minimo de 0}

Beachten Sie in Zeile 12, dass wir die Möglichkeit haben, die Daten mit der Addition der Differenzfunktion f (analog_value) auszudrucken.

Schritt 22: Verwenden der PolySolve-Korrekturfunktion

Hier verwenden wir die PolySolve-Funktion innerhalb der Arduino-IDE.

/* Modus: normal Polynom Grad 6, 2365 x, y Datenpaare Korrelationskoeffizient (r^2) = 9, 907187626418e-01 Standardfehler = 1, 353761109831e+01 Ausgabeform: C/C++ Funktion: Copyright © 2012, P. Lutus -- https://www.arachnoid.com. Alle Rechte vorbehalten. */ double f(double x) { return 2.202196968876e+02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow(x, 2) + -3.470360275448e-07 * pow(x, 3) + 2.082790802069e- 10 * pow(x, 4) + -5,306931174991e-14 * pow(x, 5) + 4,787659214703e-18 * pow(x, 6); }

Beachten Sie die Komma-zu-Punkt-Änderung als Dezimaltrennzeichen.

Schritt 23: Capture mit Korrektur - Plotter Serial

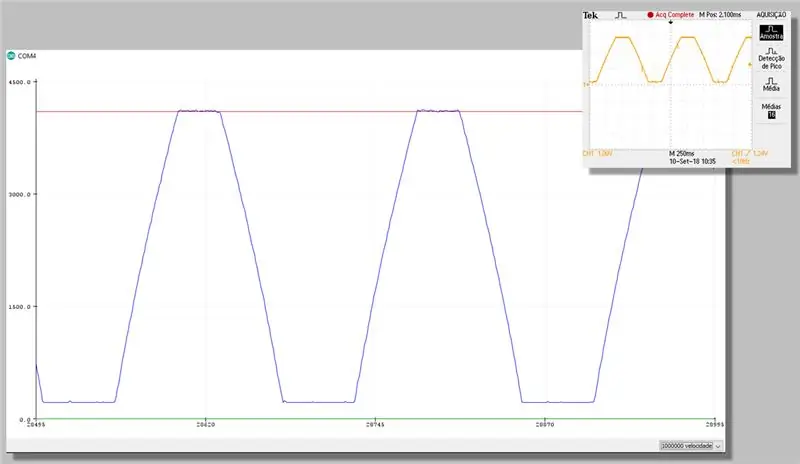
Schritt 24: Rechenkosten

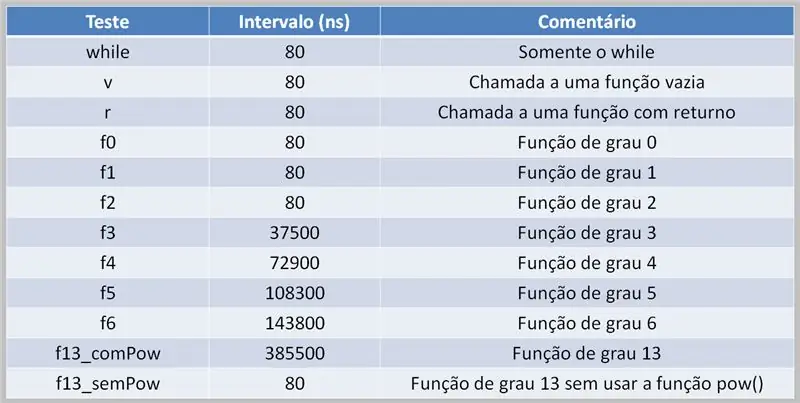
Um Polynomberechnungen durchzuführen, muss der Prozessor diese Aufgabe übernehmen. Dies kann je nach Quellcode und verfügbarer Rechenleistung zu Verzögerungen bei der Ausführung führen.

Hier sehen wir eine Ergebnistabelle eines Tests mit mehrstufigen Polynomen. Beachten Sie den Unterschied zwischen den Zeiten, in denen die Funktion pow() verwendet wurde und wann nicht.

Schritt 25: Testcode - Setup () und Loop Start ()

Hier haben wir den Code, der in unserem Test verwendet wurde.

Void setup () { Serial.begin (1000000); // Iniciando ein Porta Serial Somente Para Debug} Void Schleife () { Float valor_analogico = 500.0; // um valor arbtrario float quantidade = 10000.0; //quantidade de chamadas float contador = 0.0; //contador de chamadas

Schritt 26: Testcode - Schleife () und Verarbeitung

Ich habe die Funktion micros() verwendet, um den Wert in Mikrosekunden zu erhalten.

//============= inicia oder processo float agora = micros(); //marca o instante inicial while (contador <quantidade) { //v(valor_analogico); //função vazia //r(valor_analogico); //função com retorno //f0(valor_analogico); //grau 0 //f1(valor_analogico); //grau 1 //f2(valor_analogico); //grau 2 //f3(valor_analogico); //grau 3 //f4(valor_analogico); //grau 4 //f5(valor_analogico); //grau 5 //f6(valor_analogico); //grau 6 //f13_semPow(valor_analogico); //grau 13º SEM a função POW //f13_comPow(valor_analogico); //grau 13º COM ein função POW contador++; } agora = (micros() - agora)/quantidade; //determina o intervalo que se passou para cada iteração //============= finaliza o processo

Schritt 27: Testcode - Schleife () - Ergebnisse

Wir drucken den von der Note 13-Funktion zurückgegebenen Wert mit und ohne POW zum Vergleich sowie das Verarbeitungsintervall.

// Imprime o valor retornado da função de grau 13 com e sem POW für den Vergleich Serial.print (f13_semPow (valor_analogico)); // grau 13º SEM ein função POW Serial.print (" - "); Serial.print (f13_comPow (valor_analogico)); // grau 13º COM ein função POW Serial.print (" - "); // imprime o intervalo do processamento Serial.println (agora, 6); }

Schritt 28: Testcode - Verwendete Funktionen

Leere Funktionen (nur mit Rückgabe) von Grad 0 und 1.

//FUNÇÃO VAZIAdouble v(double x) {} //FUNÇÃO SOMENTE COM RETORNO double r(double x) { return x; } //FUNÇÃO DE GRAU 0 double f0(double x) { return 2.202196968876e+02; } //FUNÇÃO DE GRAU 1 double f1(double x) { return 2.202196968876e+02 + 3.561383996027e-01 * x; }

Funktionen der Klassen 2, 3 und 4.

//FUNÇÃO DE GRAU 2double f2(double x) { return 2.202196968876e+02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow(x, 2); } //FUNÇÃO DE GRAU 3 double f3(double x) { return 2.202196968876e+02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow(x, 2) + -3.470360275448e-07 * pow(x, 3); } //FUNÇÃO DE GRAU 4 double f4(double x) { return 2.202196968876e+02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow(x, 2) + -3.470360275448e-07 * pow(x, 3) + 2,082790802069e-10 * pow(x, 4); }

Funktionen der Klassen 5 und 6.

//FUNÇÃO DE GRAU 5double f5(double x) { return 2.202196968876e+02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow(x, 2) + -3.470360275448e-07 * pow(x, 3) + 2,082790802069e-10 * pow(x, 4) + -5,306931174991e-14 * pow(x, 5); } //FUNÇÃO DE GRAU 6 double f6(double x) { return 2.202196968876e+02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow(x, 2) + -3.470360275448e-07 * pow(x, 3) + 2,082790802069e-10 * pow(x, 4) + -5,306931174991e-14 * pow(x, 5) + 4,787659214703e-18 * pow(x, 6); }

Klasse 13-Funktion mit dem POW.

//FUNÇÃO DE GRAU 13 USANDO O POWdouble f13_comPow(double x) { return 2, 161282383460e+02 + 3, 944594843419e-01 * x + 5, 395439724295e-04 * pow(x, 2) + -3, 968558178426e-06 * pow(x, 3) + 1, 047910519933e-08 * pow(x, 4) + -1, 479271312313e-11 * pow(x, 5) + 1, 220894795714e-14 * pow(x, 6) + -6, 136200785076e-18 * pow(x, 7) + 1, 910015248179e-21 * pow(x, 8) + -3, 566607830903e-25 * pow(x, 9) + 5, 000280815521e-30 * pow(x, 10) + 3, 434515045670e-32 * pow(x, 11) + -1, 407635444704e-35 * pow(x, 12) + 9, 871816383223e-40 * pow(x, 13); }

Funktion der Klasse 13 ohne POW.

//FUNÇÃO DE GRAU SEM USAR O POWdouble f13_semPow(double x) { return 2, 161282383460e+02 + 3, 944594843419e-01 * x + 5, 395439724295e-04 * x * x + -3, 968558178426e-06 * x * x * x + 1, 047910519933e-08 * x * x * x * x + -1, 479271312313e-11 * x * x * x * x * x + 1, 220894795714e-14 * x * x * x * x * x * x + -6, 136200785076e-18 * x * x * x * x * x * x * x + 1, 910015248179e-21 * x * x * x * x * x * x * x * x + -3, 566607830903e- 25 * x * x * x * x * x * x * x * x * x + 5, 000280815521e-30 * x * x * x * x * x * x * x * x * x * x + 3, 434515045670e- 32 * x * x * x * x * x * x * x * x * x * x * x + -1, 407635444704e-35 * x * x * x * x * x * x * x * x * x * x * x * x + 9, 871816383223e-40 * x * x * x * x * x * x * x * x * x * x * x * x * x; }

Schritt 29: Dateien

Laden Sie die Dateien herunter:

PDF

INO

Kalkulationstabelle