Inhaltsverzeichnis:
- Schritt 1: Librerías importieren
- Schritt 2: Evalua La Función
- Schritt 3: Asigna-Variablen De Las Coordenadas
- Schritt 4: Construcción Del Trapecio Según Coordenadas Y Función
- Schritt 5: Calcular El Área Del Trapecio Dentro De La Función
- Schritt 6: Gráfica En Pyplot
- Schritt 7: Organización De La Gráfica
- Schritt 8: Lo Lograste
- Autor John Day day@howwhatproduce.com.
- Public 2024-01-30 07:17.
- Zuletzt bearbeitet 2025-01-23 12:52.
Antes que nada, para desarrollar este programa debes instalar la plataforma Python desde su página oficial:. Es ist empfehlenswert, die Version 2.7.12 von 64 Bit zu installieren.
Schritt 1: Librerías importieren

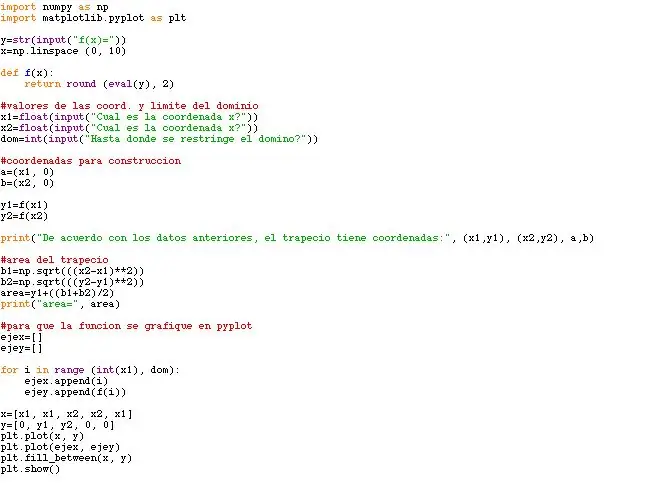
Este programa requiere dos librerías dentro del programa: matplotlib.pyplot y pylab. En la foto adjunta a este paso se puede ver que haciendo uso de los comandos from, import y as el programa puede acceder a la información de las dos liberías usadas por este programa.
aus pylab-Import
import matplotlib.pyplot als plt
WICHTIG: POR FAVOR NO PONGAS TILDES EN NINGUNA PALABRA NI NINGÚN SÍMBOLO DEL ESPAÑOL! DE LO CONTRARIO SE CERRARÁ EL PROGRAMA Y NO SE GUARDARÁN LOS CAMBIOS QUE HICISTE
Schritt 2: Evalua La Función

Hay ciertas cosas que no puedes calcular sin sabre ciertos datos que el programa no te puede dar, a menos que le preguntes al usuario (es decir el que va a utilizar el programa después de su creación) los valores de ciertas variables; en este caso debemos preguntarle al usuario por la función a la cual le quieras calcular el área.
Para preguntarle al usuario por el tipo de función, debes hacer uso de los comandos stream (str) e input. stream es un comando que allowe introducir variables algebraicas (como "x" y "y") dentro de un conjunto numérico y que se entiendan como números desconocidos dentro de la ecuación, es decir que allowe calcular, por ejemplo, x^2 y que entienda a "x" como un número que no se conoce. Por otro lado, Eingabegenehmigung que el valor que introduzcas cuando el programa pregunte por la variable sea el que adquiera el resto del programa. La función linspace sirve para restringir los valores del eje a los indicados dentro del paréntesis.
En este caso, se necesita definir la variable "y" por medio de una función
y=str(eingabe("f(x)="))
x=np.linspace (0, 10) def f(x): Rückgaberunde (eval(y), 2)
Schritt 3: Asigna-Variablen De Las Coordenadas

Para que las coordenadas cartesianas se puedan graficar, es ist notwendig, que el programa pregunte al usuario los valores que toma la función en el eje x. Dado que estos son valores valores enteros, se debe volver a usar input, que Permite que el valor que introduzcas cuando el programa pregunte por la variable sea el que adquiera de el resto del programa. Para que el programa pregunte las variables cuando lo pongas a funcionar, debes usar print para que la pregunta aparezca en la ventana SHELL. En este caso, se necesita sabre los dos valores de x y la restricción del dominio.
Recuerda que el dominio son los valores del eje x en una función.
#valores de las coord. y limite del dominiox1=float(input("Cual es la coordenada x?")) x2=float(input("Cual es la coordenada x?")) dom=int(input("Hasta donde se restringe el domino?"))
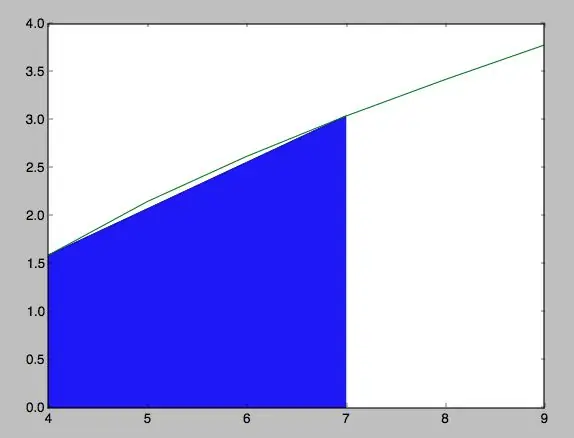
Schritt 4: Construcción Del Trapecio Según Coordenadas Y Función

Para construir el polígono, ya se tienen los valores que adquiere la función en x. Ahora, para los valores de y y (x1, 0) y (x2, 0), se le asigna con las variables y=f(x) y otro nombre para las previamente mencionadas.
#coordenadas para construcciona=(x1, 0) b=(x2, 0) y1=f(x1) y2=f(x2)
print("De acuerdo con los datos anteriores, el trapecio tiene coordenadas:", (x1, y1), (x2, y2), a, b)
Schritt 5: Calcular El Área Del Trapecio Dentro De La Función
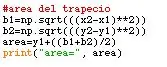
Para este paso, se debe tener en cuenta la forma del trapecio, es decir, que tiene dos bases y la altura. Las bases en este caso se obtienen por medio de la raíz cuadrada de la resta de los valores de x1 y x2 al cuadrado. Lo mismo ocurre para los valores de y1 y y2.
Para hallar el área total, es la suma de la altura y las bases sobre dos.
#area del trapeciob1=np.sqrt(((x2-x1)**2)) b2=np.sqrt(((y2-y1)**2)) area=y1+((b1+b2)/2) print ("Bereich=", Bereich)
Schritt 6: Gráfica En Pyplot

#para que la funcion se grafique en pyplot
ejex=
ey=
für i im Bereich (int(x1), dom):
ejex.append(i) ejey.append(f(i))
Para que la función se grafique hay que asignar los ejes x & y, pero como ya hay muchas Variablen mit esos nombres, asigna unos que identifiques como los ejes y no otras Variablen. El condicional for i in range organiza la función de acuerdo con los parámetros establecidos al inicio del programa.
Schritt 7: Organización De La Gráfica

x=[x1, x1, x2, x2, x1]y=[0, y1, y2, 0, 0]
plt.plot(x, y)
plt.plot(ejex, ejey) plt.fill_between(x, y) plt.show()
En este paso se organizan las coordenadas de manera que coincidan con la gráfica en sus respektivos ejes. Por otro lado, es donde se rellena el espacio del trapecio en donde se va a calcular el área y se muestra la gráfica.
Schritt 8: Lo Lograste
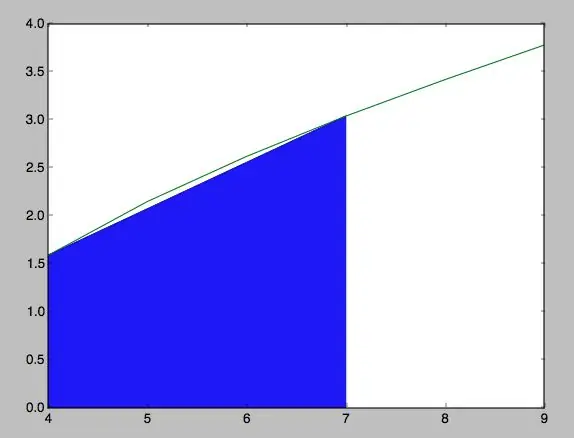

Después de haber seguido todos los pasos, encontrarás que tu debe ser muy ähnlich wie que hay und las fotos adjuntas. Obviamente, los valores de las coordenadas y la función según como to quieras ponerlos, y por ende, el área y la forma de la la curva.
Empfohlen:
So erstellen Sie Ihre erste einfache Software mit Python – wikiHow

So erstellen Sie Ihre erste einfache Software mit Python: Hallo, willkommen zu diesem Instructables. Hier werde ich erzählen, wie Sie Ihre eigene Software erstellen. Ja, wenn Sie eine Idee haben… aber wissen, wie Sie neue Dinge umsetzen können oder daran interessiert sind, Neues zu schaffen, dann ist es das Richtige für Sie
COVID19-Dashboard auf Weltkarte (mit Python) – wikiHow

COVID19-Dashboard auf der Weltkarte (mit Python): Ich weiß, dass fast alle von uns die meisten Informationen über COVID19 kennen , ich habe das Programm zum Github-Repository hinzugefügt: https://github.co
Experimente in der erweiterten Datenprotokollierung (mit Python): 11 Schritte

Experimente in der erweiterten Datenprotokollierung (mit Python): Es gibt viele Anleitungen zur Datenprotokollierung. Als ich also ein eigenes Protokollierungsprojekt erstellen wollte, habe ich mich bei einem Haufen umgesehen. Einige waren gut, andere nicht so sehr, also beschloss ich, einige der besseren Ideen aufzunehmen und meine eigene Bewerbung zu machen. Dieses Ergebnis
Einen Würfel mit Python würfeln – wikiHow
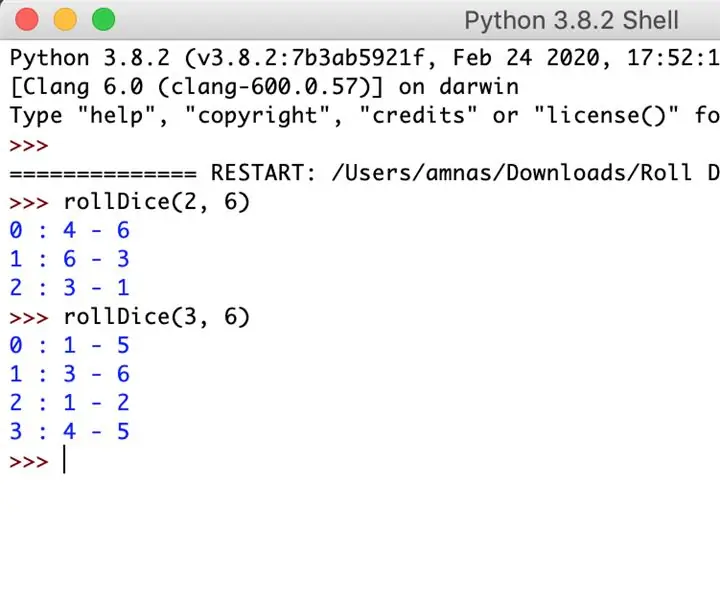
So würfeln Sie mit Python: Die folgenden Anweisungen zeigen Ihnen, wie Sie ein Python-Modul zum „Würfeln“erstellen. Dieses Modul generiert Zufallszahlen aus diesen computerisierten Würfeln. Ich werde Funktionen bereitstellen, die zum Erstellen des Moduls erforderlich sind und eine Beschreibung als
So erstellen Sie eine While-Schleife in Python – wikiHow

So erstellen Sie eine While-Schleife in Python: Es gibt Momente in der Programmierung, in denen Sie eine Reihe von Schritten wiederholen müssen, um ein Problem zu lösen. Mit einer while-Schleife können Sie einen Codeabschnitt durchlaufen, ohne wiederholten Code schreiben zu müssen. Beim Programmieren immer wieder den gleichen Code schreiben
