DIY Laser-Lenkmodul für Arduino - Gunook

2024 Autor: John Day | [email protected]. Zuletzt bearbeitet: 2024-01-30 07:21

In diesem Instructable werde ich den Bau eines zweiachsigen Einspiegel-Laserstrahl-Lenkmoduls mit 3D-gedruckten Teilen und kostengünstigen Komponenten von eBay demonstrieren.

Dieses Projekt hat Ähnlichkeiten mit Arduino Laser Show mit voller XY-Steuerung und Arduino Laser Show mit echten Galvos, aber ich glaube, es ist das erste, das ein 3D-gedrucktes Design mit kostengünstigen Magnetspulen verwendet. Ich stelle alle Designdateien unter die GPLv3, damit das Design verbessert und verbessert werden kann.

Obwohl ich derzeit nur das Modul zusammengebaut und einen sehr einfachen Testcode geschrieben habe, hoffe ich, dass ich es eines Tages auf die nächste Stufe bringen kann, indem ich den Vektorgrafikcode aus meinem früheren Instructable, Super Fast Analog Voltages von Arduino einbeziehe.

Schritt 1: Sammeln Sie die nicht-3D-gedruckten Teile

Die Laserbaugruppe besteht aus folgenden Teilen:

• 4 Mikromagnete
• Ein 1/2 Zoll Spiegel
• Vier M3-Schrauben

Die von mir verwendeten Magnetspulen wurden bei eBay für jeweils 1,45 US-Dollar gekauft. Der runde Spiegel wurde in der HobbyLobby im Bastelgang gefunden – eine Packung mit 25 Stück kostete mich weniger als 3 Dollar. Spiegel finden Sie auch bei eBay.

Sie benötigen auch einen preiswerten Laserpointer von eBay. Ein violetter Laser zusammen mit einer im Dunkeln leuchtenden Vinylplatte ist eine ausgezeichnete Kombination für dieses Projekt!

Ein Satz helfender Hände ist nicht erforderlich, aber sehr nützlich, um den Laserpointer zu halten und zu positionieren. Ein großer Bindeclip kann verwendet werden, um den Einschaltknopf gedrückt zu halten.

Sie benötigen einen Arduino (ich habe einen Arduino Nano verwendet) und eine Möglichkeit, die Magnetspulen anzutreiben. Wie VajkF in den Kommentaren angegeben hat, können Sie vorgefertigte H-Brücken verwenden, wie sie auf der L298 oder der L9110 basieren. Diese sind bei eBay für ein paar Dollar leicht erhältlich und können auch für Antriebsmotoren und Robotikprojekte verwendet werden.

Da ich keine H-Brücke hatte, baute ich meinen eigenen Treiber aus diskreten Komponenten:

• Vier NPN-Bipolartransistoren (ich habe einen MPS3704)
• Vier Widerstände (ich habe einen 1,2k Ohm Widerstand verwendet)
• Vier Dioden (ich habe einen 1N4004 verwendet)
• Eine 9V Batterie und Batterieanschluss

Die elektronischen Komponenten stammen aus meinem Labor, daher habe ich keine genauen Kosten dafür, aber es sei denn, Sie haben die Teile bereits oder können sie bereinigen, ist es wahrscheinlich kostengünstiger, eine vorgefertigte H-Brücke zu verwenden. Trotzdem werde ich die Schaltpläne für den eigenen Bau zur Verfügung stellen.

Schritt 2: 3D-Druck des Spiegellenkungsmoduls

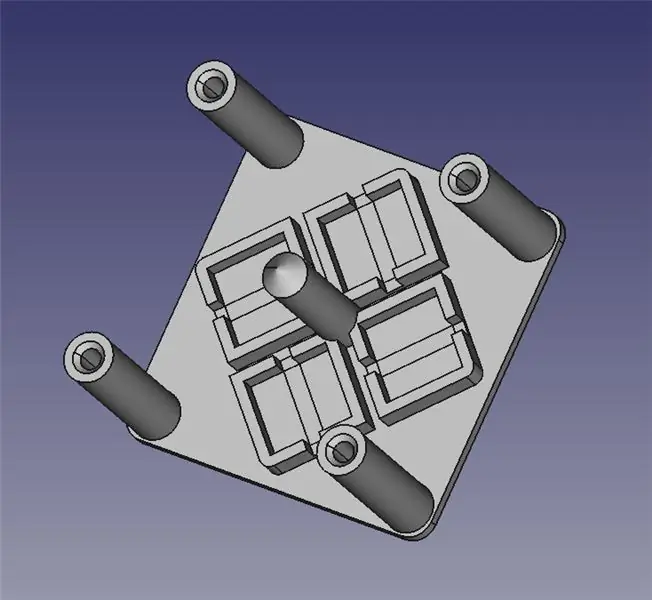
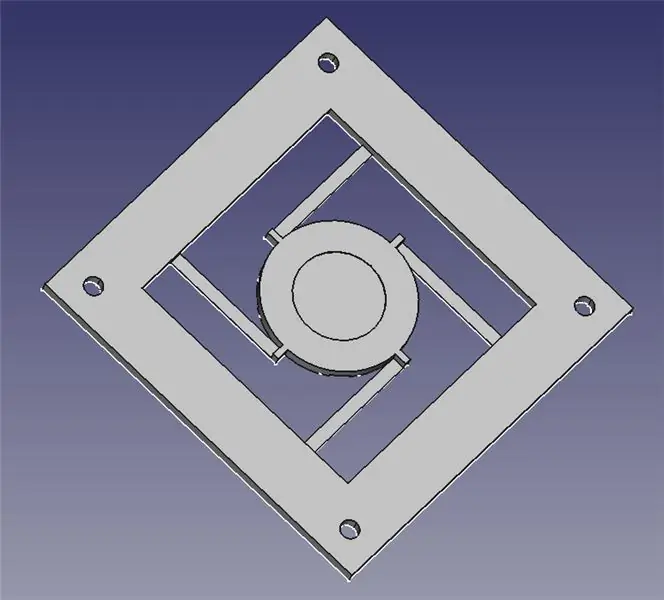
Das Laser-Lenkungsmodul besteht aus zwei 3D-gedruckten Teilen: einer Basis zur Montage von vier Magnetspulen und einer Gelenkplattform für den Spiegel.

Ich habe die beiden STL-Dateien für Sie an den 3D-Druck angehängt, sowie FreeCAD-Dateien, falls Sie das Design ändern müssen. Alle Inhalte stehen unter der GPLv3, es steht Ihnen also frei, Ihre Verbesserungen vorzunehmen und zu teilen!

Schritt 3: Zusammenbau des Lasermoduls

• Verwenden Sie Heißkleber, um die vier Magnetspulen am unteren Teil zu befestigen.
• Verwenden Sie Heißkleber, um den Spiegel in der Mitte des Oberteils zu befestigen.
• Setzen Sie die Metallkolben in die Magnetspulen ein und positionieren Sie dann das Oberteil auf den Pfosten (aber nicht festschrauben). Drehen Sie das Oberteil leicht und heben Sie jeden Kolben mit einem kleinen Schraubendreher in Position. Die Lippe der Scheibe sollte in die Nut am Kolben gleiten. Seien Sie vorsichtig, da die 3D-gedruckten Scharniere sehr zerbrechlich sind. Mit Geduld und eventuell ein paar Fehlversuchen sollte man alle vier Kolben ohne Verdrehen oder Druck auf die Scharniere positionieren können.
• Sobald alle Kolben positioniert sind, setzen Sie die M3-Schrauben teilweise ein, aber bevor Sie sie festziehen, drücken Sie jeden Kolben vorsichtig nach unten und stellen Sie sicher, dass sich der Spiegel frei neigt. Wenn es sich nicht frei bewegt oder einrastet, kann es erforderlich sein, die obere Platte zu entfernen, einen oder mehrere Magnetspulen abzuhebeln und in einem leichten Winkel nach außen wieder anzubringen (das Anbringen von Distanzstücken zwischen ihm und dem Mittelpfosten kann dabei helfen)..

Schritt 4: Drucken Sie das Laserpointer-Halsband

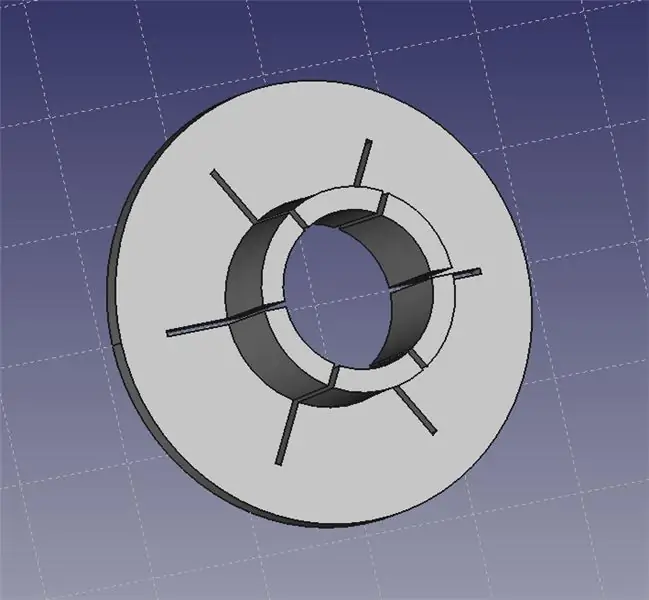
Der Kragen des Laserpointers passt auf den Kopf des Laserpointers. Sie können dann mit einem Satz helfender Hände das Halsband greifen und den Laser präzise auf Ihrer Bank positionieren.

Schritt 5: Bauen Sie die Fahrschaltung zusammen

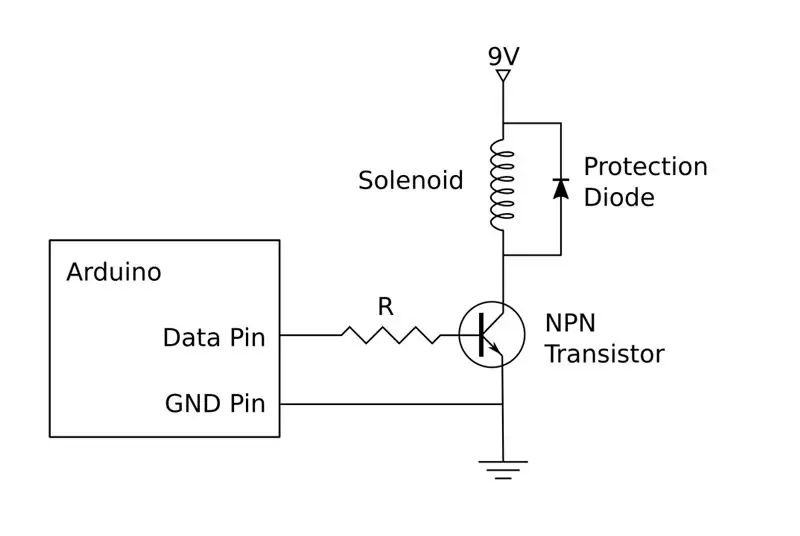
Die Ansteuerschaltung ist im Schaltplan dargestellt. Wie bereits erwähnt, besteht meine Version aus diskreten Komponenten, Sie können jedoch auch eine leicht verfügbare H-Brücke verwenden. Wenn Sie sich entscheiden, Ihre eigene zu bauen, müssen Sie vier Kopien dieser Schaltung bauen, eine für jeden der vier Magnetspulen.

Jeder Stromkreis wird mit einem Arduino-Pin verbunden, zwei für die Steuerung des linken und rechten Solenoids und zwei für die Auf- und Ab-Magnetspulen. Diese müssen wie folgt mit PWM-fähigen Pins verbunden werden:

• Pin 9: Aufwärts-Magnetventil
• Pin 3: Abwärtsmagnet
• Pin 11: Linkes Magnetventil
• Pin 10: Rechter Magnet

Eine einzelne 9-V-Batterie kann zum Antreiben aller vier Magnetspulentreiberkreise verwendet werden, oder Sie können ein Tischnetzteil verwenden. Der Arduino wird mit USB-Strom betrieben und sollte nicht an die positive Seite der 9V-Batterie angeschlossen werden. Die negative Seite der Batterie wird jedoch als Massereferenz verwendet und sollte sowohl mit dem GND-Pin des Arduino als auch mit den Emitter-Pins der Transistoren verdrahtet werden.

Schritt 6: Laden Sie den Beispielcode hoch

Der Beispielcode wurde mit den folgenden Funktionen aktualisiert:

• Passt die PWM-Frequenz so an, dass der Mechanismus bei niedrigen Geschwindigkeiten nahezu geräuschlos ist. Das Brummen in Motion Test 1 ist komplett weg!
• Addiert als Spannungsgleichungen basierend auf dem Papier von Schimpf, um das nichtlineare Verhalten der Magnetspulen zu "linearisieren".

Ich habe auch eine Implementierung eines Lorenz Attractors basierend auf dem Code aus diesem Blog eingefügt.

Die Genauigkeit der Ergebnisse lässt zu wünschen übrig, aber ich arbeite noch daran!:)

Die folgenden Schritte veranschaulichen einige der im Code verwendeten Techniken.

Schritt 7: Lautstärke verringern

In meinem Bewegungstest 1 ist ein lautes Summen zu hören, insbesondere bei Auf- und Abbewegungen. Es stellte sich heraus, dass dies dadurch verursacht wurde, dass die standardmäßige PWM-Chopping-Frequenz des Arduino im hörbaren Bereich lag. Das schnelle Ein- und Ausschalten der Spulenspannung würde sie in dieser Frequenz zum Schwingen bringen und sie zu winzig kleinen Lautsprechern machen.

Um dieses Problem zu lösen, habe ich die PWM-Frequenz im Code erhöht:

#define PWM_FREQ_31372Hz 0x01 // Setzt die PWM-Frequenz auf 31372,55 Hz#define PWM_FREQ_3921Hz 0x02 // Setzt die PWM-Frequenz auf 3921,16 Hz #define PWM_FREQ_980Hz 0x03 // Setzt die PWM-Frequenz auf 980,39 Hz void setPWMTimerFrequencies. CR1 & 0b11111000) | Frequenz; // Setze Timer1 (Pins 9 & 10) Frequenz TCCR2B = (TCCR2B & 0b11111000) | Frequenz; // Stellen Sie die Frequenz von Timer2 (Pins 3 & 11) ein}

Das Einstellen der Arduino-PWM-Frequenz ist ein nützlicher Trick, um Magnetspulen oder Motoren zu beruhigen. Experimentieren Sie mit den verschiedenen Frequenzen, um zu sehen, welche Ihnen die besten Ergebnisse liefert. Obwohl es etwas fortgeschrittenere Programmierung erfordert, finden Sie hier eine gute Ressource zur Funktionsweise der Timer.

Schritt 8: Abstimmung der Spannungen zur Reduzierung von Verzerrungen

Meine ersten Bewegungstests zeigten, dass die Reaktion der Magnetspulen erheblich verzerrt war. In Motion Test 3 (linke Abbildung) wurde aus einer eigentlich kreisförmigen Spirale stattdessen ein rechteckiges Netz mit gezackten Kanten.

Um dieses Problem zu lösen, war ein wenig Mathematik erforderlich, aber ich konnte im Internet eine erstaunliche Arbeit finden, die mir half, das Problem gut genug zu verstehen, um es in Software zu lösen.

Was folgt, führt Sie durch den Prozess, den ich durchlaufen habe, um das System zu optimieren und das Erscheinungsbild der resultierenden Spuren zu verbessern!

Schritt 9: Perfektionieren der Software mit Math

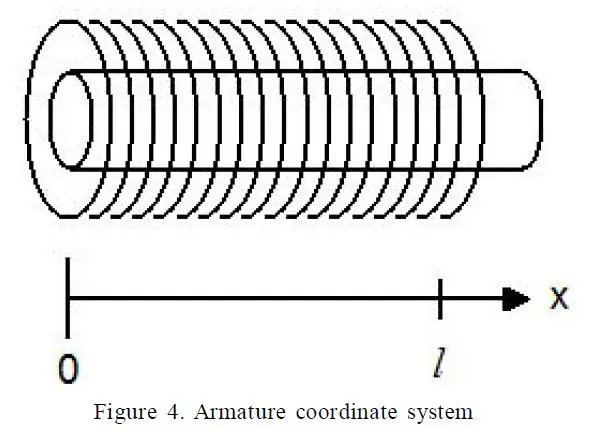
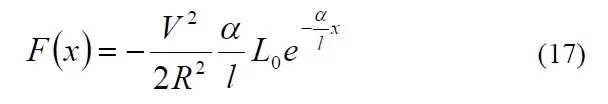
Als Geheimnis der Systemabstimmung erwies sich ein exzellentes Papier mit dem Titel "A Detailed Explanation of Solenoid Force" von Paul H. Schimpf von der Eastern Washington University (Link). Insbesondere gab mir Gleichung 17 die Solenoidkraft in Bezug auf verschiedene Ausdrücke.

Die folgenden Begriffe waren leicht zu messen:

• R - Der Widerstand meines Solenoids
• l - Die Länge des Magneten
• x - Die Verschiebung des Kolbens im Magneten
• V - Die Spannung am Magnetventil

Ich wusste auch, dass die vom Magneten abgegebene Kraft die Kraft der 3D-gedruckten Federn auf dem zweiachsigen Spiegel ausgleichen musste. Die Kraft einer Feder wird durch das Hookesche Gesetz bestimmt, das wie folgt lautet:

F = -kx

Obwohl ich den Wert von k nicht kannte, wusste ich zumindest, dass die Kraft, die ich aus der Gleichung 17 aus Schimpfs Arbeit erhielt, der Kraft aus dem Hookeschen Gesetz entsprechen musste.

Der Wert von Alpha (α) war schwierig. Obwohl die Gleichungen 13 und 14 zeigten, wie diese Werte aus der Fläche des Solenoids (A), der Windungszahl (N) und den magnetischen Permeabilitätswerten (μ) berechnet werden, wollte ich kein Solenoid zerreißen müssen, um die Anzahl der Umdrehungen, noch kannte ich das Material, aus dem der Kern meines Solenoids bestand.

Schritt 10: Ein kostengünstiger Komponententester rettet den Tag

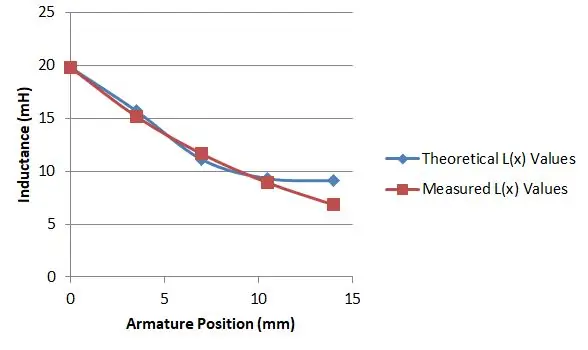
Es stellte sich jedoch heraus, dass die Gleichungen 15 und 16 mir das gaben, was ich brauchte. Ich hatte einen preiswerten M328-Komponententester, den ich bei eBay für 10 US-Dollar gekauft hatte. Es war in der Lage, damit die Induktivität meines Magneten zu messen, und ich stellte fest, dass ich durch Einschieben des Ankers in verschiedenen Tiefen unterschiedliche Induktionswerte erhielt.

Die Messung mit vollständig eingesetztem Anker ergab den Wert von L(0).

Die Länge meines Solenoids betrug 14 mm, also habe ich die Induktivität mit dem Anker an fünf Positionen gemessen und dies gab mir verschiedene Werte für L (x):

• L(0,0) = 19,8 mH
• L(3,5) = 17,7 mH
• L(7,0) = 11,1 mH
• L(10,5) = 9,3 mH
• L(14) = 9,1 mH

Ich habe dann eine Tabelle verwendet, um meine Werte gegen den Wert der Gleichungen 15 und 16 für eine bestimmte Auswahl von μr darzustellen, und dann meine Auswahl variiert, bis ich eine gute Übereinstimmung gefunden habe. Dies geschah, als μr 2,9 betrug, wie in der Grafik gezeigt.

Schritt 11: Finden Sie die Federkonstante K, lösen Sie das Problem

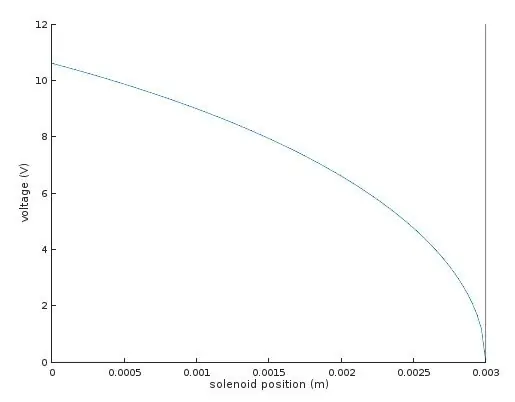
Die einzige verbleibende Unbekannte war K, die Federkonstante. Ich habe dies gemessen, indem ich 9V an einen der Magnetspulen in meiner zweiachsigen Baugruppe angelegt und den Abstand gemessen habe, in dem der Spiegel heruntergezogen wurde. Mit diesen Werten konnte ich die Gleichungen für K lösen, die meiner Meinung nach bei 10,41 liegen.

Ich hatte jetzt die Werte, die ich brauchte, um den Zug des Magneten an verschiedenen Positionen entlang des Hubs zu berechnen. Indem ich F(x) gleich der Federkraft aus dem Hookeschen Gesetz setze, kann ich nach der erforderlichen Spannung V auflösen.

Das Diagramm zeigt die Spannung, die erforderlich ist, um den Magneten in jede gewünschte Position x zu bewegen.

Rechts, wo die Spannung Null ist und die Position 3 mm beträgt, entspricht dies dem neutralen Ruhepunkt des Magneten, wenn die 3D-gedruckten Scharniere vollständig entspannt sind. Das Bewegen nach links in der Grafik entspricht dem Ziehen des Ankers in den Magneten gegen den Zug der 3D-gedruckten Scharniere – dies erfordert zunächst mehr Spannung, aber wenn der Anker tiefer in den Magneten eindringt, nimmt der Zug zu und die erforderliche Antriebsspannung verjüngt sich.

Diese Beziehung ist definitiv nichtlinear, aber mit den Gleichungen aus Schimpfs Papier kann ich meinen Arduino-Code schreiben, um die richtigen Spannungen auszugeben, damit die Strahlablenkung linear ist:

float positionToVoltage(float x) {

// Rückstellkraft durch Scharniere (Hooke's Law) bei gewünschtem x. const float spring_F = -spring_K * (x - spring_X0); // Spannung so, dass die Zugkraft des Magneten der // Rückstellkraft der Scharniere entspricht return sqrt(-2*R*R*(-spring_F)*solenoid_len/(a*L_0*exp(-a*x/solenoid_len))); }

Dies führt zu einer viel kreisförmigeren Spirale als in meinem ursprünglichen Bewegungstest. Mission erfüllt!

Schritt 12: Fragen und Antworten zur Treiberschaltung mit diskreten Komponenten

Warum kann ich das Solenoid nicht direkt an den Arduino anschließen?

Es kommt darauf an, wie viel Strom das Arduino liefern kann, ohne Schaden zu nehmen. Das sind ca. 40mA pro Pin. Da wir wissen, dass der Arduino mit 5 V arbeitet, können wir das Ohmsche Gesetz verwenden, um den erforderlichen Mindestwiderstand der Last (in diesem Fall des Solenoids) zu berechnen. Die Division von 5 Volt durch 0,040 Ampere ergibt 125 Ohm. Wenn die Last einen größeren Widerstand hat, können wir sie direkt an das Arduino anschließen, sonst können wir es nicht. Ein kleines Solenoid hat normalerweise einen Widerstand von 50 Ohm, so dass wir es nicht direkt vom Arduino antreiben können. Wenn wir es täten, würde es 100 mA ziehen, was eindeutig zu viel ist.

Warum verwenden Sie 9V für das Solenoid, aber 5V für das Arduino?

Der Arduino läuft mit 5V, aber das ist etwas zu wenig für ein Solenoid. Die Verwendung eines Transistors ermöglicht es uns, eine Spannung für das Solenoid auszuwählen, die unabhängig von den für das Arduino verwendeten 5 V ist.

Woher weiß ich, ob ein Transistor für dieses Projekt geeignet ist?

Genau wie beim Arduino besteht die Hauptanforderung darin, dass der durch das Solenoid fließende Strom die maximalen Nennwerte für den Transistor (insbesondere den Kollektorstrom) nicht überschreitet. Wir können das Worst-Case-Szenario leicht berechnen, indem wir den Widerstand des Solenoids messen und dann die Versorgungsspannung dadurch teilen. Bei 9V Versorgungsstrom für die Magnetspulen und einem Magnetspulenwiderstand von 50 Ohm liegen wir im Worst-Case-Szenario bei 180mA. Der MPS3704 zum Beispiel ist für einen maximalen Kollektorstrom von 600 mA ausgelegt, was uns einen Spielraum von etwa 3 ergibt.

Wie bestimme ich den Mindestwert des Widerstands zwischen dem Arduino-Ausgang und der Basis des Transistors?

Der Ausgang des Arduino verbindet den Basisschenkel der Bipolartransistoren über einen Strombegrenzungswiderstand. Da der Arduino mit 5 V arbeitet, können wir wieder das Ohmsche Gesetz verwenden, um den Widerstand zu berechnen, der erforderlich ist, um den Strom unter 40 mA zu begrenzen. Das heißt, 5 Volt durch 0,04 Ampere teilen, um einen Wert von mindestens 125 Ohm zu erhalten. Höhere Widerstandswerte verringern den Strom und geben uns somit eine noch größere Sicherheitsmarge.

Gibt es einen Maximalwert für diesen Widerstand, den ich nicht überschreiten sollte?

Es stellt sich heraus, ja. Ein Transistor hat eine sogenannte Stromverstärkung. Wenn die Verstärkung beispielsweise 100 beträgt, bedeutet dies, dass, wenn wir 1 mA in die Basis stecken, bis zu 100 mA durch die Last fließen, die der Transistor steuert. Wenn wir 1,8mA in den Sockel stecken, dann fließen bis zu 180mA durch die Last. Da wir früher berechnet haben, dass bei 9 V 180 mA durch das Solenoid fließen, ist ein Basisstrom von 1,8 mA der "Sweet Spot" und weniger und unser Solenoid schaltet sich nicht vollständig ein.

Wir wissen, dass der Arduino 5 V ausgibt und wir wollen, dass 1,8 mA Strom fließen, also verwenden wir das Ohmsche Gesetz (R = V / I), um den Widerstand (R = V / I) zu berechnen. 5V geteilt durch 1,8mA ergibt einen Widerstand von 2777 Ohm. Unter Berücksichtigung der von uns getroffenen Annahmen erwarten wir also, dass der Widerstand zwischen 125 und 2777 liegen muss – die Wahl von etwa 1000 Ohm gibt uns in beiden Fällen eine ziemlich gute Sicherheitsmarge.

Schritt 13: Analyse aktueller Probleme und möglicher Lösungen

Der aktuelle Prototyp zeigt Potenzial, aber es bleiben mehrere Probleme:

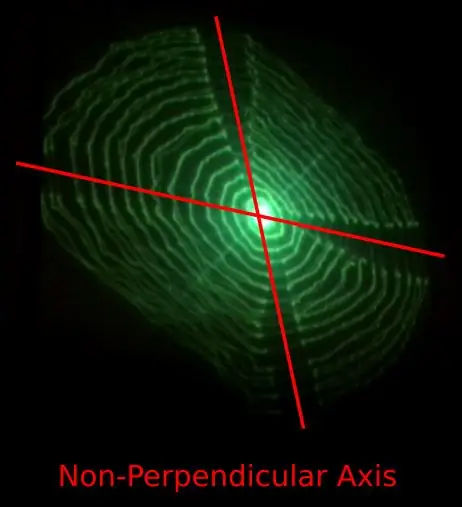
1. Die Bewegung entlang der X- und Y-Achse scheint nicht senkrecht zu sein.
2. Es gibt einen Sprung, wenn der Spiegel die Richtung ändert.
3. Die Auflösung ist recht gering und es gibt sichtbare Treppenstufenmuster.
4. Bei höheren Bewegungsgeschwindigkeiten wird der Weg des Lasers durch Vibrationen und Klingeln verzerrt.

Problem 1) kann durch das Design der 3D-gedruckten flexiblen Scharniere verursacht werden, die Bewegungen entlang einer Achse auf die senkrechte Achse übertragen.

Problem 2) ist auf ein Spiel in der Kopplung zwischen den Antriebskolben und der Spiegelplattform zurückzuführen, dies führt dazu, dass der Spiegel an den Übergängen zwischen der X- und Y-Achse ruckelt und überspringt. Diese plötzliche Bewegung führt zu einer abgedunkelten X-förmigen Lücke, in der der Laserpunkt eine schnellere unkontrollierte Bewegung ausführt.

Problem 3) tritt auf, weil die Standard-Arduino-PWM nur 255 Stufen hat und einige davon aufgrund der Form der Spannungskurve verschwendet werden. Dies könnte durch die Verwendung von Timer1 erheblich verbessert werden, der 16 Bit hat und 65536 eindeutige Werte aufnehmen kann.

Problem 4) tritt auf, weil der Spiegel und der Gleitanker (Kolben) des Magnetventils eine erhebliche Menge an bewegter Masse darstellen.

Da die Punkte 1) und 2) mit der mechanischen Konstruktion zusammenhängen, besteht eine Möglichkeit darin, die metallischen Kolben zu entfernen und durch kleine Seltenerd-Magnete zu ersetzen, die direkt auf der Kippscheibe befestigt werden. Die Magnetspulen wären eine offene Spule, die die Magnete anziehen oder abstoßen würde, ohne physischen Kontakt herzustellen. Dies würde zu einer gleichmäßigeren Bewegung führen und die Möglichkeit von Ruckeln beseitigen, während die Gesamtmasse reduziert wird.

Die Reduzierung der Masse ist die primäre Lösung für Problem 4), aber alle verbleibenden Probleme könnten direkt in der Software angegangen werden, indem ein Bewegungssteuerungsprofil in die Software implementiert wird, um den Spiegel kontrolliert zu beschleunigen und abzubremsen. Dies ist in der 3D-Drucker-Firmware bereits weit verbreitet und ähnliche Methoden könnten auch hier funktionieren. Hier sind einige Ressourcen zur Bewegungssteuerung in Bezug auf 3D-Drucker:

• "Mathematik von Motion-Control-Profilen", Chuck Lewin (Link)
• "Ruckgesteuerte Bewegung erklärt", (Link)

Ich vermute, dass das Hinzufügen eines trapezförmigen Bewegungssteuerungsprofils es ermöglichen würde, den Spiegel mit viel höheren Geschwindigkeiten ohne Klingeln oder Vibrationsartefakte zu fahren.

Schritt 14: Zukünftige Arbeiten und mögliche Anwendungen

Obwohl die Entwicklung von Lösungen für diese Probleme einen erheblichen Arbeitsaufwand erfordern wird, hoffe ich, dass dieses Open-Source-Beam Steering-Modul eine erschwingliche Alternative zu galvanometerbasierten Projekten in folgenden Anwendungen werden kann:

• Eine preiswerte Lasershow für DJs und VJs.
• Ein elektromechanisches Vektordisplay für ein klassisches Arcade-Spiel wie das Vectrex.
• Ein DIY-SLA-3D-Drucker vom Harztyp, der im Geiste der RepRap-Bewegung ein eigenes Laser-Lenkungsmodul drucken kann.
• Digitales Schwenken oder optische Bildstabilisierung für Kameras.

Zweiter Preis beim Arduino Contest 2017