So messen Sie Hochfrequenz und Duty Cycle gleichzeitig mit einem Mikrocontroller. - Gunook

2025 Autor: John Day | [email protected]. Zuletzt bearbeitet: 2025-01-13 06:56

Ich weiß, was Sie denken: "Huh? Es gibt viele Anleitungen zur Verwendung von Mikrocontrollern zur Messung der Signalfrequenz. Gähnen." Aber warten Sie, es gibt eine Neuheit in diesem: Ich beschreibe eine Methode zur Messung von Frequenzen, die viel höher sind als ein Mikrocontroller (MCU) und das Tastverhältnis des Signals - alles gleichzeitig!

Der Frequenzbereich des Geräts reicht von ~43 Hz bis ~450 kHz, während das Tastverhältnis von 1 % bis 99 % reicht.

Lassen Sie mich den Teil "kann es ertragen" erklären: Eine MCU misst die Periode eines Rechteckwellensignals T, indem sie die Zeit zwischen zwei aufeinanderfolgenden Übergangsereignissen verfolgt. Zum Beispiel springt die Spannung von niedriger zu hoher Spannung an einem seiner I/O-Pins. Es tut dies, indem es die Anzahl der Impulse seiner eigenen internen Uhr zählt. Naiverweise sollte die Obergrenze für gemessene Frequenzen dem Nyqvist-Shannon-Abtasttheorem gehorchen; h., es würde ungefähr der Hälfte der Taktfrequenz der MCUs entsprechen. In Wirklichkeit ist die Grenze viel, viel niedriger, weil die MCU Code ausführen muss, um Interrupts zu verarbeiten, Variablen zu speichern, arithmetische Operationen durchzuführen, Ergebnisse anzuzeigen usw. In meinen Experimenten mit einer 48-MHz-MCU war die minimale Anzahl von Taktzyklen zwischen messbaren Übergängen etwa 106. Somit wäre die obere Grenze des messbaren Frequenzbereichs in diesem Fall 48.000 / 212 / 2 = 226,4 kHz.

Während die MCU die Periode des Signals misst, kann sie auch ihre Pulsbreite bestimmen, P: die Zeit, in der die Signalspannung hoch bleibt. Mit anderen Worten, die Zeit zwischen Low-to-High- und High-to-Low-Übergängen. Das Tastverhältnis des Signals wird dann als folgender Prozentsatz definiert:

Duty = 100 % * P / T

Genau wie bei der Frequenz gibt es eine praktische Grenze für die Pulsbreite. Bei Verwendung des obigen Beispiels würden 106 Taktzyklen die Pulsbreite auf nicht weniger als 2,21 Mikrosekunden begrenzen. Oder nicht weniger als 50% bei 226,4 kHz.

Eine Möglichkeit, die obere Frequenzgrenze von Rechtecksignalen anzuheben, ist die Anwendung von digitalen Teilern, die Flip-Flops verwenden. Eine Division der Eingangsfrequenz durch n würde den messbaren oberen Bereich um das n-fache erweitern. Das sind großartige Neuigkeiten, digitale Teiler haben einen grundlegenden Fehler: Das geteilte Signal verliert die Pulsbreite (und das Tastverhältnis)! Aufgrund der Arbeitsweise der Teiler hat deren Ausgang immer 50% Duty Cycle. Schade…

Auf den folgenden Seiten werde ich jedoch zeigen, wie man die Frequenz digital teilt und die ursprüngliche Pulsbreite beibehält, so dass ich Signale weit über die Grenzen hinaus messen kann, die durch direktes Zählen auferlegt werden.

Schritt 1: Digitale Frequenzteilung

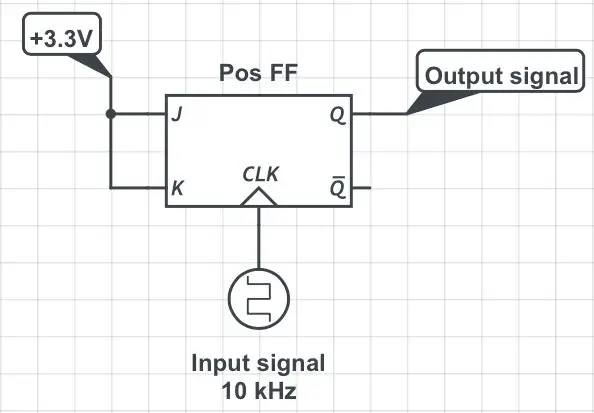
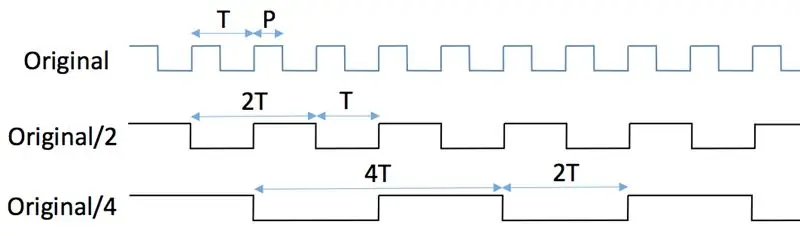
Herkömmliche digitale Frequenzteiler verwenden Flip-Flops; Dieses Tutorial erklärt schön die Prinzipien, wie man Teiler mit Standard-JK-Flip-Flops baut. Dies löst das Problem der zu hohen Eingangsfrequenzen für die MCU, hat jedoch einen großen Nachteil: Das geteilte Signal hat unabhängig von der Einschaltdauer des Eingangssignals 50% Tastverhältnis! Um zu sehen, warum das so ist, schauen Sie sich die ersten beiden Zahlen an. Das Originalsignal mit Periode T und Pulsbreite P wird in den Taktpin eines JK-Flip-Flops eingespeist, während dessen J- und K-Pins ständig auf High gehalten werden (erste Abbildung). Es wird durchgehend eine 3,3-V-Logik angenommen. Nehmen wir an, das Flip-Flop wird durch die positive (d. h. steigende) Flanke des Taktgebers getriggert. Unter diesen Bedingungen treten Änderungen des Zustands des Ausgangspins (einzelne "Flips" und "Flops") jedes Mal auf, wenn der Taktpin von niedrig auf hoch geht. Der Hoch-Tief-Übergang des Takts (d. h. die negative Flanke) wird vollständig ignoriert. Siehe die zweite Abbildung. Der Ausgangspin Q gibt ein Signal aus, dessen Periode doppelt so lang ist wie die ursprüngliche Periode, d. h. seine Frequenz ist halbiert. Die Pulsbreite des Ausgangs ist immer gleich T. Folglich geht die ursprüngliche Pulsbreite P verloren.

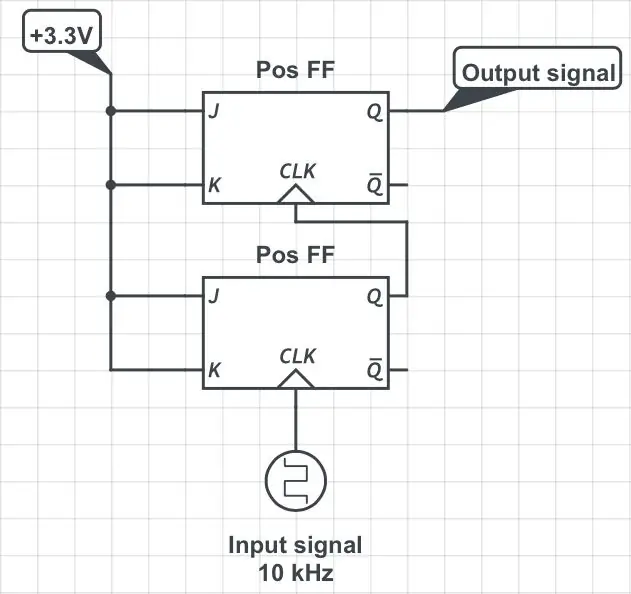
Das Hinzufügen eines weiteren JK-Flip-Flops in einer in der dritten Abbildung gezeigten Konfiguration teilt die ursprüngliche Frequenz durch 4. Das Hinzufügen weiterer Flip-Flops auf dieselbe sequentielle Weise teilt die Frequenz durch nachfolgende Potenzen von 2: 8, 16, 32 usw.

Problem: Wie teilt man die Frequenz einer Rechteckwelle unter Beibehaltung ihrer Pulsbreite?

Die Idee ist, dem Mix ein durch eine negative Flanke ausgelöstes JK-Flipflop richtig hinzuzufügen. Nennen wir es "Neg FF"; siehe vierte Abbildung. "Richtig" bedeutet hier, dass die J- und K-Pins des neuen Flip-Flops mit den Q- bzw. Qbar-Ausgangspins des Teilers durch 4 ("Pos FF") verbunden sind, der in der vorherigen Abbildung dargestellt ist. (Hier ist "bar" der horizontale Balken über dem Q-Symbol, der eine logische Negation anzeigt.) Um zu sehen, was dies bewirkt, sehen Sie sich die Funktionstabelle des "Neg FF" in der fünften Abbildung an: Negs Ausgangspins, Q und Qbar, spiegeln den Zustand seiner Eingangspins J bzw. K. Das heißt, sie spiegeln den Zustand von Q und Qbar von Pos wider. Die Flip-Flop-Aktion des Neg muss jedoch auf die negative Flanke des ursprünglichen Signals warten, die zum Zeitpunkt P nach der positiven Flanke ankommt. Aha!

Die resultierenden Wellenformen sind in der sechsten Abbildung dargestellt. "Pos Q" gibt das Signal mit der 1/4-Frequenz aus, "Pos Qbar" ist invers, "Neg Q" folgt auf "Pos Q" verschoben um die Pulsbreite P und "Neg Qbar" ist seine Umkehrung. Sie können überprüfen, dass das logische UND von "Pos Qbar" und "Neg Q" eine Impulsfolge erzeugt, die durch die ursprüngliche Impulsbreite P und 1/4 der Frequenz gekennzeichnet ist. Bingo!

Anfangs habe ich genau dieses Ausgangssignal verwendet, um die MCU zu speisen. Bei sehr kurzen Pulsbreiten stellte sich dies jedoch aufgrund der in der Einleitung erwähnten 106-Zyklen-Begrenzung der MCU als problematisch heraus. Ich habe dieses kleine Problem gelöst, indem ich stattdessen eine andere Ausgabe ausgewählt habe: "Pos Qbar" UND "Neg Qbar". Ein Blick auf die Wellenformen sollte Sie davon überzeugen, dass die Pulsbreite dieser speziellen Wellenform, P', zwischen T und 2T statt im (0, T)-Bereich für P variiert. Das P kann leicht aus P' wiederhergestellt werden durch:

P = 2T - P'

Schritt 2: Empfohlene Hardware

Ich mag wirklich den relativen Neuling unter den elektronischen Bastlern: Atmel SAM D21 MCUs basierend auf dem 32-Bit ARM Cortex M0+ Prozessor, der mit 48 MHz Taktfrequenz arbeitet, viel höher als die älteren Atmels. Für dieses Projekt habe ich gekauft:

• ItsyBitsy M0 Express MCU-Board von Adafruit
• Ich hatte zufällig einen wiederaufladbaren LiPo-Akku von Adafruit
• Monochromes 128x32 SPI OLED-Display (Sie haben es erraten: Adafruit)
• Duales positiv flankengetriggertes JK-Flipflop SN74HC109 von Texas Instruments
• Duales negativ flankengetriggertes JK-Flipflop SN74HC112 von Texas Instruments
• Vierfach-UND-Gatter CD74AC08E von Texas Instruments
• Vierfach-ODER-Gatter CD74AC32E von Texas Instruments

Schritt 3: Die Schaltung

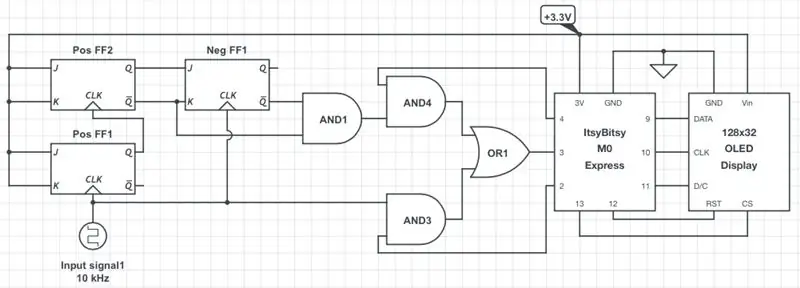
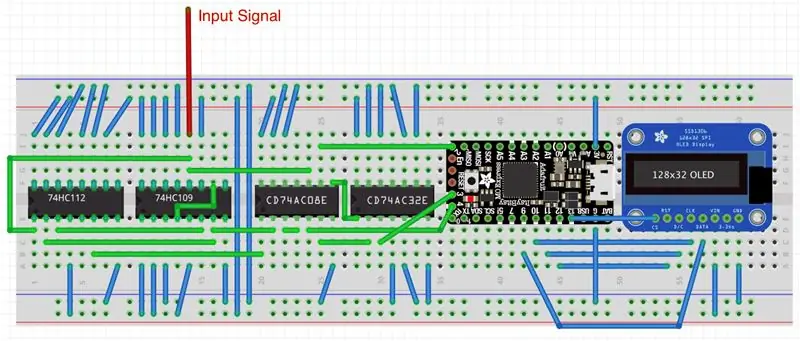
Die erste Abbildung zeigt ein vereinfachtes Schema des Frequenz-/Duty-Meters. Es wird durchgehend die 3,3-V-CMOS-Logik angenommen. Folglich muss die Amplitude der Eingangsrechteckwelle zwischen den entsprechenden V_{ICH H} (d. h. 2 V) und 3,3 V. Wenn nicht, müssen Sie es entsprechend nach oben oder unten skalieren. In den meisten Fällen würde ein einfacher Spannungsteiler ausreichen. Wenn Sie Ihre Version des Zählers auf einer anderen Logikebene gestalten möchten, müssen Sie einen anderen Mikrocontroller (MCU), eine Batterie und ein Display verwenden, die auf der gewünschten Ebene funktionieren. Die in diesem Projekt verwendeten Logikgatter und Flip-Flops arbeiten mit Logikpegeln zwischen 2 V und 6 V und sollten in den meisten Fällen in Ordnung sein.

Wie gezeigt verwendet die ItsyBitsy-MCU die Pins 9-13, um über das Software-SPI-Protokoll mit dem Display zu kommunizieren. Der 3V-Pin versorgt die gesamte Schaltung mit Strom. Der digitale Eingang Pin 3 akzeptiert das analysierte Signal, während die Pins 2 und 4 die Signalquelle steuern: entweder direktes Signal, das durch Gate AND3 (niedrige Eingangsfrequenzen) kommt, oder Signal durch 4 geteilt durch Gate AND4 (hohe Eingangsfrequenzen), wie in Schritt 2 beschrieben Der im nächsten Schritt besprochene Code erkennt automatisch den eingehenden Frequenzbereich und schaltet die Signalquelle entsprechend um.

Der Schaltplan zeigt nicht die wahre Komplexität digitaler Chipverbindungen. Das zweite Bild zeigt, wie das Projekt auf einem Steckbrett aussehen würde. Das Eingangssignal kommt über einen roten Draht zum 2CLK-Pin des dualen Flipflops mit positiver Flanke. ACHTUNG: Normalerweise sollten alle J- und K-Pins dieses Flip-Flops hoch gehalten werden, aber insbesondere SN74HC109 verfügt stattdessen über den Kbar-Pin - einen invertierten K-Pin. Daher muss dieser Pin geerdet werden! Das erste Flip-Flop mit negativer Flanke in SN74HC112 hat seinen 1K- und 1J-Pin mit den 1Q- und 1Qbar-Pins von SN74HC109 verbunden. Das zweite Flip-Flop im SN74HC112 ist unbenutzt und seine Eingangspins (2K, 2J, 2CLRbar) sind geerdet. Alle anderen zusätzlichen Pins PREbar (Preset) und CLRbar (Clear) in allen Flip-Flops müssen mit logisch hoch verbunden sein. Nicht verwendete Takt- und Ausgangspins bleiben unbeschaltet. Ebenso werden ungenutzte Eingangspins in allen Gattern geerdet, während ungenutzte Ausgangspins unverbunden bleiben. Wie ich in meinem "Invisible Killer of the Phone Ring" Instructable besprochen habe, beseitigt das Erden ungenutzter Eingangspins von logischen Chips zufällige Schwingungen und spart Batteriestrom.

Schritt 4: Der Code und das Messen niedriger Frequenzen

Natürlich geschieht die gesamte Aktion in dem unten verlinkten Code. Wenn der an Pin 3 eingehende Eingang von digital niedrig auf hoch umschaltet, beginnt die MCU, die Impulse ihres internen 48-MHz-Takts zu zählen. Es merkt sich den Moment des Übergangs von hoch zu niedrig und setzt die Zählung bis zum nächsten Wechsel von niedrig zu hoch fort, wenn es den gesamten Prozess erneut startet. Die erste Zählung stellt die Impulsbreite dar, während die gesamte Zählung die Periode des Signals darstellt. Und das ist das ganze Geheimnis.

Die CPU merkt sich diese Übergänge über Prozessalarme. Der SAMD21 hat mehrere Takte; Mein Code verwendet TC3. Anfangs habe ich damit begonnen, das Datenblatt des M0 zu lesen, um viel Mühe beim Codieren des Interrupt-Handlers zu haben, aber bald habe ich einen sehr verwandten Code in den Arduino-Foren-Beiträgen der Benutzer electro_95, MartinL und Rucus entdeckt, deren Beitrag ist gebührend anerkannt. Ich habe ihren kombinierten Code in meinen eingebaut und modifiziert; spart mir viel zeit!

Wie ich bereits erwähnt habe, ist die Signalauflösung auf ~106 CPU-Zyklen begrenzt, um Code zwischen Interrupts auszuführen. Die digitale Teilung mit Pulsbreitenerhaltung kümmert sich um hohe Frequenzen. Niedrige Frequenzen hingegen stellen eine weitere Herausforderung dar: Da der TC3-Taktzähler 16 Bit lang ist, läuft er nach dem Überschreiten der 65.536-Zählgrenze über. Man kann mit dieser Situation umgehen, indem man einen Überlauf-Interrupt hinzufügt, wählt aber eine andere Lösung: TC3 kann einen vorskalierten (d. h. durch Software geteilten) CPU-Takt anstelle des Hardwaretakts von 48 MHz verwenden. Wenn sich also die Periode des Signals der Überlaufgrenze nähert, kann der Code TC3 anweisen, 24 MHz-Zählungen für die nächste Periode zu verwenden, und voilà, der Zähler fällt unter 32.768 Zählungen. Für noch niedrigere Frequenzen kann der TC3 angewiesen werden, 12-MHz-Impulse usw. zu zählen. Der geeignete Vorteiler wird automatisch basierend auf der Frequenz des Signals mit Hysterese bestimmt, um den TC3-Zähler innerhalb der Überlaufgrenze zu halten. Damit liegt das untere Ende des Gerätebereichs bei etwa 43 Hz.

Sie können den Code gerne forken und in Ihrem Projekt verwenden, aber bitte geben Sie bei der Veröffentlichung der Ergebnisse die Quelle an.

Link zum Code.