Wahrheitstabellen lösen - Gunook

2024 Autor: John Day | [email protected]. Zuletzt bearbeitet: 2024-01-30 07:16

Eine Wahrheitstabelle ist eine Möglichkeit, alle Ergebnisse eines Problems zu visualisieren. Dieser Befehlssatz ist für Anfänger gedacht, die in die diskrete Mathematik einsteigen. Wir üben heute mit einem Beispielproblem, das spezifisch für diese Anleitung ist. Sie benötigen etwas Kratzpapier und einen Bleistift, um die Tabelle zu visualisieren. Dieses Problem sollte für Personen mit Vorkenntnissen zum Thema etwa 5 Minuten und für Anfänger etwa 10 Minuten dauern.

Für diesen Befehlssatz konzentrieren wir uns auf das Problem ~p Λ q. Wir verwenden dies, um einige Symbole einzuführen, die zur Interpretation von Wahrheitstabellen erforderlich sind.

Schritt 1: Wahrheitstabellen verstehen

Eine Wahrheitstabelle ist eine Möglichkeit, alle Möglichkeiten eines Problems zu visualisieren. Die Kenntnis von Wahrheitstabellen ist eine Grundvoraussetzung für die diskrete Mathematik. Hier finden wir alle Ergebnisse für die einfache Gleichung von ~p Λ q.

Schritt 2: Die Symbole kennen

Der erste Schritt zur Wahrheitstafel besteht darin, die Zeichen zu verstehen. Das „~“in diesem speziellen Problem steht für Negation. „p“und „q“sind beide Variablen. Das „Λ“entspricht „und“. Diese Gleichung wird als „nicht p und q“gelesen, was bedeutet, dass die Gleichung wahr ist, wenn p nicht wahr ist und q wahr ist.

Schritt 3: Formatieren der Tabelle

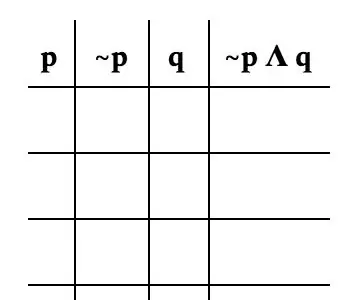
Jetzt die eigentliche Tabelle bilden. Es ist wichtig, das Problem nach jeder Variablen aufzuschlüsseln. Für dieses Problem werden wir es wie folgt aufteilen: p, ~p, q und ~p Λ q. Das Bild ist ein gutes Beispiel dafür, wie Ihr Tisch aussehen sollte.

Schritt 4: Zuweisen von Wahr und Falsch

Da es nur zwei Variablen gibt, gibt es nur vier Möglichkeiten pro Variable. Für p teilen wir es mit der Hälfte der Leerzeichen auf, die von T (für wahr) und die andere Hälfte von F (für falsch) eingenommen werden.

Schritt 5: Negation

Für ~p schreiben Sie das entgegengesetzte Vorzeichen, das p hat, da ~p das Gegenteil von p ist.

Schritt 6: Variable "q"

Für q wechselt man zwischen T und F, um jede mögliche Kombination zu erhalten. Da sich die Gleichung nur auf ~p konzentriert, können wir die p-Spalte ignorieren, wenn wir die Wahrheit der Gleichung bestimmen. Das Symbol „Λ“bedeutet, dass sowohl ~p als auch q wahr sein müssen, damit die Gleichung wahr ist.

Schritt 7: Auflösen nach False in der letzten Spalte

Da für die erste Zeile ~p F ist und q T ist, ist ~p Λ q F in dem Szenario, dass ~p F ist und q T ist. Das einzige Szenario, in dem die Gleichung T lautet, ist, wo ~p T und q ist T.

Schritt 8: Finden des Wahren in der letzten Spalte

Dies bedeutet, dass die einzige Zeile, die T ist, die dritte ist.

Schritt 9: Fertigstellen der Tabelle

Überprüfen Sie, ob Ihre Tabelle korrekt ist. Sie tun dies, indem Sie überprüfen, ob Ihre Zeichen richtig sind, und sicherstellen, dass die letzte Spalte korrekt ist. Die letzte Spalte ist das Ergebnis aller möglichen Permutationen aus den Variablen.

Schritt 10: Fertig

Jetzt, da Sie wissen, wie man eine grundlegende Wahrheitstabelle erstellt, üben Sie weiter! Je mehr Sie üben, desto besser werden Sie darin werden.