Einfacher Autorange-Kondensatortester / Kapazitätsmesser mit Arduino und von Hand - Gunook

2024 Autor: John Day | [email protected]. Zuletzt bearbeitet: 2024-01-30 07:19

Hallo!

Für diese Physik-Einheit benötigen Sie:

* ein Netzteil mit 0-12V

* ein oder mehrere Kondensatoren

* ein oder mehrere Ladewiderstände

* eine Stoppuhr

* ein Multimeter zur Spannungsmessung

* ein Arduino-Nano

* ein 16x2 I²C-Display

* 1/4W Widerstände mit 220, 10k, 4.7M und 1Gohms 1Gohms Widerstand

* Dupont-Draht

Schritt 1: Allgemeine Informationen zu Kondensatoren

Kondensatoren spielen in der Elektronik eine sehr wichtige Rolle. Sie werden verwendet, um Ladungen zu speichern, als Filter, Integrator usw. Aber mathematisch gesehen steckt viel in Kondensatoren. So können Sie Exponentialfunktionen mit Kondensatoren und ihnen üben. trainieren. Wird ein zunächst ungeladener Kondensator über einen Widerstand an eine Spannungsquelle angeschlossen, so fließen kontinuierlich Ladungen zum Kondensator. Mit steigender Ladung Q steigt nach der Formel Q = C * U (C = Kapazität des Kondensators) auch die Spannung U am Kondensator. Der Ladestrom nimmt jedoch immer mehr ab, da es immer schwieriger wird, den schnell geladenen Kondensator mit Ladungen zu füllen. Die Spannung U (t) am Kondensator gehorcht folgender Formel:

U (t) = U0 * (1-exp (-k * t))

U0 ist die Spannung des Netzteils, t ist die Zeit und k ist ein Maß für die Geschwindigkeit des Ladevorgangs. Von welchen Größen hängt k ab? Je größer die Speicherkapazität (dh die Kapazität C des Kondensators) ist, desto langsamer füllt er sich mit Ladungen und desto langsamer steigt die Spannung. Je größer C, desto kleiner k. Der Widerstand zwischen Kondensator und Netzteil begrenzt auch den Ladungstransport. Ein größerer Widerstand R bewirkt, dass ein kleinerer Strom I und daher weniger Ladungen pro Sekunde zum Kondensator fließen. Je größer R, desto kleiner k. Die richtige Beziehung zwischen k und R oder C ist:

k = 1/(R * C).

Die Spannung U (t) am Kondensator steigt somit nach der Formel U (t) = U0 * (1-exp (-t / (R * C)))

Schritt 2: Die Messungen

Die Schüler sollen die Spannung U zum Zeitpunkt t in eine Tabelle eintragen und dann die Exponentialfunktion zeichnen. Wenn die Spannung zu schnell ansteigt, müssen Sie den Widerstand R erhöhen. Auf der anderen Seite, wenn sich die Spannung zu langsam ändert, verringern Sie R.

Kennt man U0, den Widerstand R und die Spannung U(t) nach einer gewissen Zeit t, so lässt sich daraus die Kapazität C des Kondensators berechnen. Dazu müsste man die Gleichung logarithmieren und nach einigen Transformationen erhalten wir: C = -t / (R * ln (1 - U (t) / U0))

Beispiel: U0 = 10V, R = 100 kOhm, t = 7 Sekunden, U(7 Sekunden) = 3,54V. Dann ergibt C einen Wert von C = 160 μF.

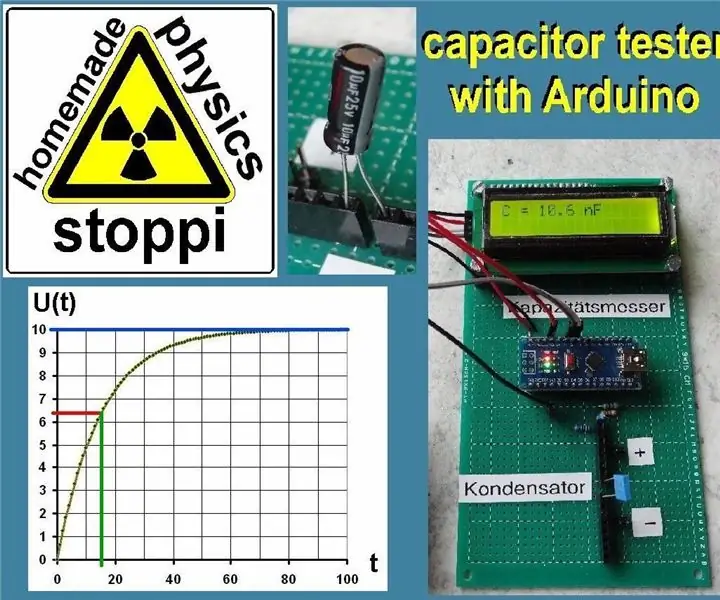
Es gibt aber noch eine zweite, einfache Methode, um die Kapazität C zu bestimmen. Die Spannung U (t) nach t = R * C beträgt nämlich genau 63,2% von U0.

U (t) = U0 * (1-exp (-R * C / (R * C)) = U0 * (1-exp (-1)) = U0 * 0,632

Was bedeutet das? Die Schüler müssen die Zeit t bestimmen, nach der die Spannung U (t) genau 63,2 % von U0 beträgt. Insbesondere für das obige Beispiel wird die Zeit gesucht, nach der die Spannung am Kondensator 10 V * 0,632 = 6,3 V beträgt. Dies ist nach 16 Sekunden der Fall. Dieser Wert wird nun in die Gleichung t = R * C eingesetzt: 16 = 100000 * C. Daraus ergibt sich das Ergebnis: C = 160 µF.

Schritt 3: Der Arduino

Am Ende der Übung kann die Kapazität auch mit einem Arduino ermittelt werden. Dies berechnet die Kapazität C genau nach der Methode von früher. Sie lädt den Kondensator über einen bekannten Widerstand R mit 5V auf und bestimmt die Zeit, nach der die Spannung am Kondensator = 5V * 0,632 = 3,16V beträgt. Für den Arduino Digital-Analog-Wandler sind 5V gleich 1023. Sie müssen also nur warten, bis der Wert des Analogeingangs 1023 * 3,16 / 5 = 647 beträgt. Mit dieser Zeit kann die Kapazität C berechnet werden. Damit Kondensatoren mit sehr unterschiedlichen Kapazitäten gemessen werden können, werden 3 verschiedene Ladewiderstände verwendet. Zunächst wird ein niedriger Widerstand verwendet, um die Ladezeit bis 647 zu bestimmen. Ist diese zu kurz, dh ist die Kapazität des Kondensators zu klein, wird der nächst höhere Ladewiderstand gewählt. Ist auch dieser zu klein, folgt am Ende der Messung ein 1-Gohm-Widerstand. Der Wert für C wird dann mit der richtigen Einheit (µF, nF oder pF) auf dem Display angezeigt.

Schritt 4: Schlussfolgerungen

Was lernen die Schüler in dieser Einheit? Sie lernen Kondensatoren, ihre Kapazität C, Exponentialfunktionen, Logarithmus, Prozentrechnungen und das Arduino kennen. Ich denke viel.

Dieses Gerät ist für Schüler im Alter von 16-17 Jahren geeignet. Sie müssen die Exponentialfunktion und den Logarithmus bereits in der Mathematik durchlaufen haben. Viel Spaß beim Ausprobieren in Ihrer Klasse und Eureka!

Ich würde mich sehr freuen, wenn Sie für mich beim Wissenschaftswettbewerb im Klassenzimmer stimmen würden. Vielen Dank dafür!

Wenn Sie sich für meine anderen Physikprojekte interessieren, hier ist mein Youtube-Kanal:

weitere Physikprojekte: